Easy-to-Use Current Limiter
CIRCUIT
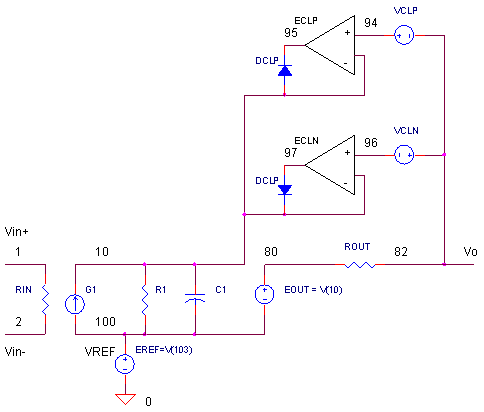
OPAMP_ILIMIT_SERVO.CIR Download the SPICE file
The output of an op amp can only deliver so much current. Ask for any more and op amp's internal clamp limits swings into action. Why? One reason is safety! Try driving lots of current into a low impedance load and you've got plenty of power to dissipate in a small plastic package.
Current limiters are typically modeled using a voltage source and a diode. Accurate limiters require knowing the max output current of the final stage, messing with the diode V-I equation and setting a clamp voltage. (See Current Limiting) But, there's an easier way. By adding an amplifier, you can create an accurate current limiter that's independent of the diode voltage or final stage current. If your output current attempts to exceed the limit, the amplifier servos the output to your maximum current. Let's see how.
CURRENT LIMITING ACTION
Suppose an op amp can only deliver ± 20 mA. Essentially, we need a limiter that work as follows.
►
For
Io_limit- < Io < Io_limit+ Normal condition - limiters out of circuit.
►
For
Io > Io_limit+
Positive servo reduces output current to Io_limit+.
►
For Io
< Io_limit- Negative servo
reduces output current to Io_limit-.
What sets Io_max? Its simply ROUT together with VCLP and VCLN.
Io_max+ = VCLP / ROUT
Io_max- = VCLN / ROUT
For an op amp with an output resistance ROUT = 10 Ω, what value of VCLP and VCLN are needed for ± 20 mA?
VCLP,VCLN = Io_limit · ROUT
= 0.02(A) · 10(Ω)
= 0.2 (V)
HOW IT WORKS
Actually, the output current is not monitored directly! Instead, its the voltage across ROUT that we observe. In reality, servo amplifiers ECLP and ECLN limit the voltage from node 10 to node 82. However, by clamping V_ROUT, the maximum output current also gets clamped.
When V_ROUT is less than VCLP and VCLN, both servo amplifiers ECLP and ECLN, are isolated from the circuit through reverse biased diodes DCLP and DCLN. That's because node 95 swings more positive and node 97 swings more negative than node 10. Under this condition, the limiter is out of the picture.
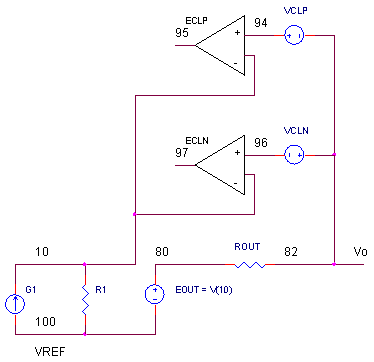
But, suppose V_ROUT rises slightly more positive than VCLP. Node 95 now swings more negative than node 10 forward biasing DCLP!
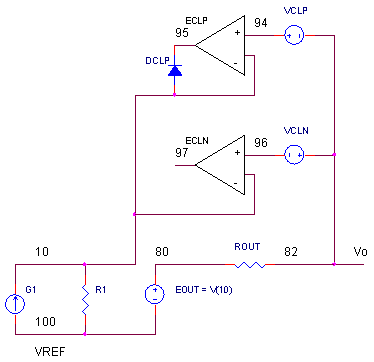
ECLP now attempts to bring down (or servos) V(10) to be equal to VCLP. You can also think of ECLP as a unity gain buffer which, during over-voltage condition, condition takes control of node 10. This is possible because R1 is typically a high impedance (>1k ohms) and the low impedance of the DVLP and EVLP can easily pull down the V(10) to VCLP or VCLN. The negative limiter works similarly, just using opposite polarities.
Note there's no diode equations to
mess with! Simply set VCLP and VCLN equal to
ROUT x Io_max = 100 ohms x 20 mA = 2V.
VCLP 94 82 DC 2V
VCLN 82 96 DC 2V
SERVO AMPS
Here are the SPICE statements for the servo amplifiers.
ECLP 95 80 94 10 1000
ECLN 97 80 96 10 1000
The input of ECLP compares V(10) - V(82) with VCLP. The servo amplifier action drives V(95) through DCLP to a level required to limit V(10) - V(82). How do we set the gain of servo amps ECLP and ECLN? For this example, the gains are set to 1000. Too high of a gain and you might have convergence problems. Too low of a gain and the limiter loses accuracy. But typically, you don't need a lot of accuracy for this function. You can even set it to 100 or less.
ROAD TEST
Let's test drive our current limited model using the non-inverting amplifier. Note, you need to connect power supplies for this model to work.
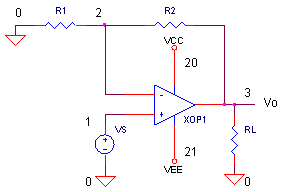
CIRCUIT INSIGHT VS generates a 5 V square wave. Run a Transient Analysis and plot the input V(1) and output V(3). With R1 = R2 = 10 kΩ, the non-inverting gain is 2 V/V. For a 5 V input, you should see a 10V output.
With VCLP = VCLN = 2 V and ROUT = 100 Ω, the output current should have a max level of VCLP / ROUT = 2 V / 100 Ω = 20 mA. The initial load resistor is RL = 100 kΩ. Open a new plot window and plot the output current I(RL). Change the load to RL = 1000 Ω. How much current flows now?
Begin decreasing RL below 1000 Ω. Rerun the simulation. Does Vo make its destination of 10 V? What's the current output? At some point Vo goes no higher. Why? Because the output current is limited to 20 mA. What is the exact output current? Place a cursor on I(RL) to get an accurate measure. (Note, some of the output current flows through R2.)
HANDS-ON DESIGN How does the servo gains effect the accuracy of Io_max? Reduce the gain of ECLP and ECLN from 1000 down to 100 or 10. Run a new simulation. How accurate is the limiting action now? Alternatively, raise the gain to 10000 or above. Did the accuracy improve?
Generally speaking, these limits don't need to be so accurate. Its not a very controlled behavior in the actual device. And furthermore, you shouldn't be designing circuits that are dependent on the accuracy of Io_max.
HANDS-ON DESIGN Try varying the current limit by adjusting VCLP, VCLN and ROUT. Run a simulation with your new values. How about asymmetric current limiting? Just set VCLP and VCLN to different levels.
SIMULATION NOTES
For a description of all op amp models, see
Op Amp Models.
For a quick review of subcircuits, check out
Why Use Subcircuits?
Get a crash course on SPICE simulation at
SPICE Basics.
A handy reference is available at SPICE
Command Summary.
This op amp model can be used for many of the op amp
circuits available from the Circuit
Collection page.
SPICE FILES
Download the file or copy this netlist into a text file with the *.cir extension.
OPAMP_ILIMIT_SERVO.CIR * * SIGNAL SOURCE VS 1 0 AC 1 PWL(0US 0V 0.01US 5V 2US 5V 2.01US -5V 4US -5V) * POWER SUPPLIES VCC 20 0 DC +15V VEE 21 0 DC -15V * NON INVERTING AMPLIFIER R1 0 2 10K R2 2 3 10K XOP1 1 2 20 21 3 OP_ILIM_S RL 3 0 100000 * OP AMP MODEL - ILIMIT SERVO *************************** * Device Pins In+ In- V+ V- Vout .SUBCKT OP_ILIM_S 1 2 101 102 82 * INPUT R RIN 1 2 1e+012 * INPUT STAGE: GAIN, POLE G1 100 10 1 2 1 R1 10 100 1e+006 C1 10 100 6.6e-008 * OUTPUT CURRENT LIMITS VCLP 94 82 DC 2 DCLP 10 95 DNOM ECLP 95 80 94 10 1000 VCLN 82 96 DC 2 DCLN 97 10 DNOM ECLN 97 80 96 10 1000 * OUTPUT STAGE EOUT 80 100 10 100 1 ROUT 80 82 100 * INTERNAL REFERENCE RREF1 101 103 100K RREF2 103 102 100K EREF 100 0 103 0 1 R100 100 0 1MEG .MODEL DNOM D .ENDS * * ANALYSIS ************************************* * .TRAN 0.05US 4US 0 0.05US *.AC DEC 20 0.1 1000MEG .PROBE .END
© 2007 eCircuit Center