Instrumentation Amplifier
Error Analysis

Step-by-Step

While the popular App Note AN-539 (Analog Devices) nicely describes and accounts for the AD623's errors, it's light on the theory and strategy behind the analysis equations. We'll do a teardown of this critical and challenging analysis. You'll get

a step-by-step approach
- walk thru each error source
- derive the circuit and sensitivity equations
- separate errors into Gain / Offset, Calibratable / Uncalibratable
an Excel file
- create, review and reuse with a systematic format
- vary parameters, see their effect on total error
- customize & expand template for your own designs

Learn more at EBA Series

AN-539

You'll find excellent descriptions of the errors sources in this App Note from Analog Devices. The actual errors are tabulated for an easy read of the results. However, the calculations are inserted into the same table without much insight. This tutorial walks through each error in an easy step-by-step approach.

OFFSET AND GAIN ERRORS

What are the basic definitions for Offset and Gain Errors of an amplifier block?

Ideal Amplifier with Gain K
- Vo = Vin*K
Actual Amplifier with errors
- Vo = Vin* (K+∆K) + ∆Voffset
∆K - Gain Error
- change in Gain from ideal (K).
- also called Slope, Span error
∆Voffset - Offset Error
- change in offset from ideal (0V)
- also called Intercept, Zero Error
Combined Offset and Gain Errors
- Error = ±∆Voffset + ( ±∆K x Reading )

MAX ERROR BUDGET

You can write the max error budget (or target spec) multiple ways. While not provided in the App Note, we'll specify a reasonable one for this analysis. Note: Sensor Full-Scale (FS) output = 20mV.

∆Voffset = 1.0% of FS + ∆K = 1.0% of Reading
∆Voffset = 0.2mV + ∆K = 1.0% of Reading
∆Voffset = 10,000ppm of FS + ∆K = 10,000ppm of Reading

INSTRUMENTATION AMP

Schematic with Error Sources

Conditions and Assumptions

Temperature

Ambient: Ta = 25C
Max change: ∆T = 60C

Sensor

Weigh Scale
Full Scale (FS) Output = 20mV
Sensor Bridge: Ra = Rb = Rc = Rd = 350 ohms,
Assume ideal. no errors for amp analysis

Amplifier Device

Analog Devices, AD623B
Signal Gain: Rg_int / Rg_ext + 1

Errors

Calibratable: Initial
Un-calibratable: Drift, Noise, Non-linearity
Errors will be Referred to Input (RTI)
Errors totaled as Worst Case (sum absolute values)
Errors due to Ibn and Ibp cancel because Ra||Rb = Rc||Rd.
Low measure bandwidth: 10Hz

OFFSET ERRORS

The Inst Amp nicely showcases the analysis method for both input and output errors. The method also shows the approach for noise and non-linearity errors.

While the steps may seem more detailed than needed for simpler errors, the value of creating a systematic approach can pay off when analyzing more complex, multi-stage designs.

INPUT OFFSET VOLTAGE

Description	Initial Errors	Drift Errors
Error Source: e	voff = 0.1mV	voff_TC = 1uV/C
Pick Analysis Node: Va	vp	vp
Calc Sensitivity: S How does e impact Va?	S = vp / voff = 1	S = vp / voff = 1
Calc Offset Error at Analysis Node Initial: ∆Voffset = e * S Drift: ∆Voffset = e * ∆T * S	∆Voffset = 0.1mV * 1	∆Voffset = 1uV/C * 60C * 1 = 0.060 mV
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = vin/vp = 1	Ka = vin/vp = 1
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 0.1mV / 1 = 0.1mV	∆voffset_RTI = 0.060mV/ 1 = 0.060mV

OUTPUT OFFSET VOLTAGE

Description	Initial Errors	Drift Errors
Error Source: e	voff_vo = 0.5mV	voff_vo_TC = 10uV/C
Pick Analysis Node: Va	vo	vo
Calc Sensitivity: S How does e impact Va?	S = vo / voff_vo = 1	S = vo / voff_vo = 1
Calc Offset Error at Analysis Node Initial: ∆Voffset = e * S Drift: ∆Voffset = e * ∆T * S	∆Voffset = 0.5mV * 1	∆Voffset = 10uV/C * 60C * 1 = 0.60 mV
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = vin/voff_vo = Rg_int / Rg_ext = 89.5	Ka = vin/voff_vo = Rg_int / Rg_ext = 89.5
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 0.5mV / 89.5 = 5.6uV	∆voffset_RTI = 0.6mV/ 89.5 = 6.7uV

INPUT OFFSET BIAS CURRENT

Description	Initial Errors	Drift Errors
Error Source: e	iboff = 2nA	iboff_TC = 5pA/C
Pick Analysis Node: Va	vp-vn	vp-vn
Calc Sensitivity: S How does e impact Va?	S = (vp-vn) / iboff = 1/2(Ra\|\|Rb+Rc\|\|Rd) = 1/2(175+175) = 175	S = (vp-vn) / iboff = 175
Calc Offset Error at Analysis Node Initial: ∆Voffset = e * S Drift: ∆Voffset = e * ∆T * S	∆Voffset = 2nA * 175 = 0.35uV	∆Voffset = 5pA/C * 60C * 175 = 0.11uV
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = Vin/vp = 1	Ka = Vin/vp = 1
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 0.35uV / 1 = 0.35uV	∆voffset_RTI = 0.11uV/ 1 = 0.11uV

OUTPUT NON-LINEARITY

Description	Calc Errors
Error Source: e (device spec at vo=4V)	vnonlin_vo = 50ppm * 4V = 0.2mV
Pick Analysis Node: Va	vo
Calc Sensitivity: S How does e impact Va?	S = vo/vnonlin_vo = 1
Calc Offset Error at Analysis Node: ∆Voffset = e * S	∆Voffset = 0.2mV * 1
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = vin/vo = Rg_int/Rg_ex + 1 = 89.5
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 0.2mV / 89.5 = 2.2uV

INPUT VOLTAGE NOISE

Description	Calc Errors
Error Source: e (device spec at 0.1 to 10Hz)	vnoise = 2.5uVp-p = 1.25uVp
Pick Analysis Node: Va	vp
Calc Sensitivity: S How does e impact Va?	S = vp / vnoise = 1
Calc Offset Error at Analysis Node: ∆Voffset = e * S	∆Voffset = 1.25uVp * 1 = 1.25uV
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = vin/vnoise = 1
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 1.25uV/1 = 1.25uV

INPUT COMMON-MODE REJECTION ERROR

Description	Calc Errors
Error Source: e	vcmr = vcm*CMRR CMRR = 105dB = 10^-105/20 = 5.6e-6
Pick Analysis Node: Va	vp
Calc Sensitivity: S How does e impact Va?	S = vp/vcmr = 1
Calc Offset Error Special Case: ∆Voffset = e * Vcm * S	∆Voffset = 5.6e-6 * 2.5V * 1 = 14uV
Calc Gain from Input to Analysis Node: Ka = Va / Vin	Ka = vin/vcmr = 1
Calc Error RTI (Referred-to-Input): ∆voffset_RTI = ∆voffset / Ka	∆voffset_RTI = 14uV/1 = 14uV

GAIN ERRORS

The differential signal gain is defined by

Gain errors often require more effort when calculating the Sensitivity S. You need to first write the gain equation and then apply calculus (Difference Method) to find S.

AN-539 skips the S calculation for gain altogether rounding it up to 1. But this only holds for high gain cases! For lower gains you could over estimate the Sensitivity (and Errors), so better to explicitly calculate S.

INTERNAL GAIN RESISTOR

Description	Initial Errors	Drift Errors
Error Source: e	Rg_int_Tol = 0.35%	Rg_int_TC = 50ppm/C = 0.0001%/C
Pick Analysis Node: Va	vo	vo
Calc Sensitivity: S How does e impact Gain K? Apply Difference Method: S = (∆K/K) / (∆R/R) where ∆K/K = (K'-K)/K	K = Rg_int/Rg_ext+1 Rg_int = 100k Rg_ext = 1.13k K = 100k/1.13k+1 = 89.5 K'=100k*1.01/1.13k+1 = 90.4 ∆R/R = 0.01 S = (∆K/K) / (∆R/R) = +0.98	S = +0.98
Calc Gain Error at Analysis Node Initial: ∆K/K = e * S Drift: ∆K/K = e * ∆T * S	∆K/K = 0.35% * 0.98 = 0.34%	∆K/K = 50ppm/C60C0.98 = 2940ppm = 0.29%
Gain errors can be referred to input node as-is, no RTI calc needed.

EXTERNAL GAIN RESISTOR

Description	Initial Errors	Drift Errors
Error Source: e	Rg_ext_Tol = 0.1%	Rg_ext_TC = 10ppm/C = 0.0001%/C
Pick Analysis Node: Va	vo	vo
Calc Sensitivity: S How does e impact Gain K? Apply Difference Method: S = (∆K/K) / (∆R/R) where ∆K/K = (K'-K)/K	K = Rg_int/Rg_ext+1 Rg_int = 100k Rg_ext = 1.13k K = 100k/1.13k+1 = 89.5 K'=100k/(1.13k*1.01)+1 = 88.6 ∆R/R = 0.01 S = (∆K/K) / (∆R/R) = -0.98	S = -0.98
Calc Gain Error at Analysis Node Initial: ∆K/K = e * S Drift: ∆K/K = e * ∆T * S	∆K/K = 0.1% * -0.98 = -0.099%	∆K/K = 10ppm/C60C-0.98 = -593ppm = -0.059%
Normalized gain errors can be referred to input node as-is, no RTI calc needed.

SUMMARY

Let's view the Gain & Offset errors as well which are Calibratable or not.

Description Error (V) (ppm)

OFFSET INITIAL    ( CALIBRATABLE )

Input Offset Voltage
Output Offset Voltage
Input Offset Bias Current
Input CMR 100 uV
6 uV
0.4 uV
14 uV 5000
279
18
703

OFFSET DRIFT, OTHER (UN-CALIBRATABLE)

Input Offset Voltage Drift
Output Offset Voltage Drift
Input Offset Bias Current Drift
Input Voltage Noise
Output Non-Linearity 60 uV
7 uV
0.1 uV
1 uV
2.2 uV 3000
335
3
38
112

GAIN INITIAL      ( CALIBRATABLE )

Rg_int_Tol
Rg_ext_Tol 0.35%
-0.098% 3461
-979

GAIN DRIFT, OTHER  (UN-CALIBRATABLE)

Rg_int_TC
Rg_ext_TC 0.28 %
-0.059 % 2966
-587

Description	Error (V)	(ppm)
OFFSET INITIAL ( CALIBRATABLE )
Input Offset Voltage Output Offset Voltage Input Offset Bias Current Input CMR	100 uV 6 uV 0.4 uV 14 uV	5000 279 18 703
OFFSET DRIFT, OTHER (UN-CALIBRATABLE)
Input Offset Voltage Drift Output Offset Voltage Drift Input Offset Bias Current Drift Input Voltage Noise Output Non-Linearity	60 uV 7 uV 0.1 uV 1 uV 2.2 uV	3000 335 3 38 112
GAIN INITIAL ( CALIBRATABLE )
Rg_int_Tol Rg_ext_Tol	0.35% -0.098%	3461 -979
GAIN DRIFT, OTHER (UN-CALIBRATABLE)
Rg_int_TC Rg_ext_TC	0.28 % -0.059 %	2966 -587

TOTALS

Errors are totalled as Worst Case (sum absolute values).

Total Error - No Cal

Offset: 0.19mV (9507 ppm)
Gain: 0.79% (7946 ppm)
Combined: 17481 ppm

Total Error - With Cal (Drift, Other Errors only)

Offset: 0.07mV (3490 ppm)
Gain: 0.35% (3554 ppm)
Combined: 741 ppm

EBA WITH EXCEL

An Excel file was created to implement the error budget analysis.

Organizes complex analyses into smaller managable sections
Easier to create, review and debug
Customizable and expandable to more complex circuits
Modular for reuse in other designs

3 Worksheets

Worksheet Enter Calculate

CIRCUIT CALC Circuit values Signal gains and error sensitivities

OFFSET Offset error sources Offset errors and totals

GAIN Gain error Sources Gain errors and totals

While 3 worksheets seems over-the-top for smaller circuits, you'll find a big advantage when analyzing more complex circuits or multi-stage systems!

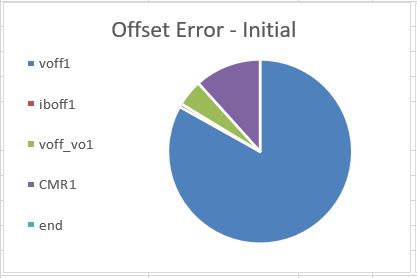
The Excel file also creates a nice graph displaying error contributions at a glance.

Dive into the hands-on spreadsheet!

Excel file: Inst_Amp_AN-539_-_Error_Budget_Analysis.xlsx
Right Click on the filename, select "Save link as..."
Open file, explore the Circuit, Offset and Gain Sheets
Play in the sandbox, modify values, see the impact on errors.
Copy to a new file - experiment!

NOTES, IDEAS...

The total error agrees closely with the original App Note. This analysis may be slightly more accurate by calculating a specific S for the gain resistors.
To add another error source, simply add another row to the OFFSET or GAIN sheets.
To add another stage, make a copy of the CIRCUIT CALC sheet and modify it for the new stage. Then add its error sources to the same OFFSET and GAIN sheets.

REFERENCES

AN-539, Errors and Error Budget Analysis in Instrumentation Amplifier Applications, Analog Devices Inc (ADI).
AD623, Single Supply, Rail-to-Rail, Low Cost Instrumentation Amplifier, Datasheet, ADI.

Back to EBA Series

Worksheet	Enter	Calculate
CIRCUIT CALC	Circuit values	Signal gains and error sensitivities
OFFSET	Offset error sources	Offset errors and totals
GAIN	Gain error Sources	Gain errors and totals

Instrumentation AmplifierError Analysis