Simplified Small Signal Model
CIRCUIT
AUDIO_SMALL_SIGNAL_MODEL.CIR Download the SPICE file
The nice thing about this simplified small-signal model is that it can tell you some major characteristics about an audio amplifier using only a handful of components. This model distills an audio amp's complexity down to a few parameters where you can predicts its gain and bandwidth. Please note, this topic applies not only to audio amps, but to its identical cousin - the op amp. In addition, the simplified model is easily expandable. If you want to explore variations of a particular stage, simply replace the simplified one with the stage that interests you and begin experimenting.
THREE SIMPLE STAGES
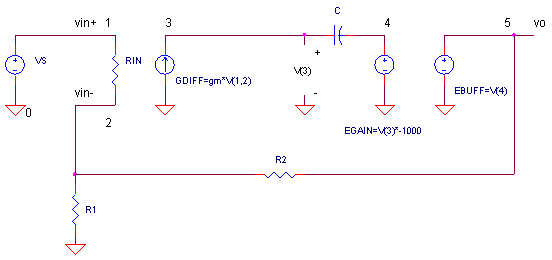
This simplified model is based on the Basic Audio Amplifier presented previously. It contains an input differential stage, a Miller Integrator, and a unity gain output buffer.
| Stage | Parameter | Small Signal Equations | |
| Differential stage | gm | I(GDIFF) = [V(1) - V(2)] · gm | |
| Miller Integrator | C | V(4) = I(GDIFF) · 1/(s · C) | |
| Unity Gain Output Buffer | V(5)=V(4) · 1 |
What is the open loop gain? You simply combine the three equations as
Aol = V(5) / [V(1) - V(2)]
= gm / (s · C)
What is the unity gain frequency? Substitute s = 2 pi f, then solve for f where the open-loop gain equals unity Aol = 1. Arrange the equation to 1 = gm / (2 · π · f · C) and solve for f.
fu = gm / (2 · π · C)
Placing the model inside a circuit with R1 and R2, you can calculate the closed loop gain as
Acl = R2 / R1 + 1.
But what is its closed-loop bandwidth, fc? You can easily predict the closed-loop bandwidth as
fc = fu / Acl
Why? If, the model has a single pole (due to the Miller Integrator), then the closed-loop gain Acl and bandwidth fc have a fixed product, fu = Acl · fc. This also commonly called the Gain Bandwidth Product. This also shows you the great gain vs. bandwidth compromise. You can have more gain Acl, but the bandwidth fc drops to keep fu constant.
SPICE TEST DRIVE
It takes only a few simple SPICE elements to build our audio amp. The input differential amp is created with an input resistor RIN and GDIFF, a Voltage Controlled Current Source (VCCS). Simply set its gain to the transconductance gm. The Miller stage looks just like one we've built before with EGAIN, a Voltage Controlled Voltage (VCVS) with high gain, and a compensation cap in the feedback. (See Miller Integrator for a quick review.) Finally, the unity gain stage EBUFF is simulated with a VCVS with a gain of 1.
Suppose you designed an audio amp with a transconductance of gm=0.02 A/V and a compensation cap of 500 pF. What are it's open loop and closed loop bandwidths?
CIRCUIT INSIGHT To test the open-loop gain, place a * at the beginning of the R2 statement. This essentially removes it from the circuit. To ground the negative input, set R1 = 1. Run an AC ANALYSIS and plot the output V(5). You should see a single pole response falling at -20 dB/dec. But, where do you expect the response to cross unity gain? A simple calculation gives you fu = gm / (2 · π · C) = 0.02 / (2 · π · 500 pF) = 6.36 MHz. Did your simulation match the calculation?
Okay, how about the closed loop gain? Set R1=1k and R2=9k for a closed
loop gain of
Acl = 9k/1k+1 = 10 V/V. What should the closed loop bandwidth be? From the
equations above, you can expect fc = fu / Aol = 6.36 MHz / 10 = 636kHz.
Rerun the simulation. Does your closed-loop gain and bandwidth hit the mark?
HANDS-ON DESIGN Okay, time to play with your audio amp's performance. Raise or lower the compensation cap by a factor of 2, or even 10. What happens to the bandwidth? Now raise or lower R2 by a similar factor. Can you predict what will happen to your bandwidth? You should be seeing the eternal trade-off between gain and bandwidth.
What if your project requires you to build an amp with both high gain and high bandwidth? You may have to spend some money on two amplifiers in cascade to achieve your goal!
Most audio amps do not have gain at DC to avoid output offset voltages that may cause large wasted DC currents to flow into speakers. Place a capacitor in series with R1 to force unity gain at DC. Rerun an AC Analysis. What is your low frequency cutoff? Adjust the cap value to move your low frequency cutoff, f_lo.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
AUDIO_SMALL_SIGNAL_MODEL.CIR * VS 1 0 AC 1 * FEEDBACK RESISTORS R1 2 0 1K R2 5 2 9K * DIFFERENTIAL STAGE RIN 1 2 1E12 GDIFF 3 0 1 2 0.02 * MILLER INTEGRATOR RIN3 3 0 1E12 C 3 4 500PF EGAIN 4 0 3 0 -1000 * BUFFER EBUFF 5 0 4 0 1 * * ANALYSIS .AC DEC 5 10 1000MEG .PROBE .END
© 2008 eCircuit Center