Op Amp Differentiator

eCircuit Center

Op Amp Differentiator - Open-Loop Analysis

CIRCUIT

OPDFR_OL.CIR Download the SPICE file

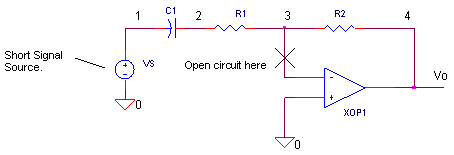
In the op amp differentiator, we find one component that's required to make it work properly - R1. Although some texts don't show it, R1 brings stability to the output. By using open-loop analysis analysis, we'll see how R1 pulls the circuit from the edge of ringing and oscillations back to the land of stability.

OPEN-LOOP ANALYSIS

Open-Loop Analysis means opening up the feedback loop and checking for danger signs in the gain and phase around the loop. What are these signs?

If there is a frequency where the AC gain around the loop is 1 V/V (0dB) and the total phase is -360 or 0 deg, then the circuit is unstable.

What are the consequences of instability? Closing the loop under these conditions creates an amplifier with a forward gain of infinity at this frequency – conditions for self-sustained oscillations. (For a review, see Op Amp Feedback Analysis.)

Performing open-loop analysis requires these three steps:

1. Short the voltage source, VS.

2. Open up the circuit.

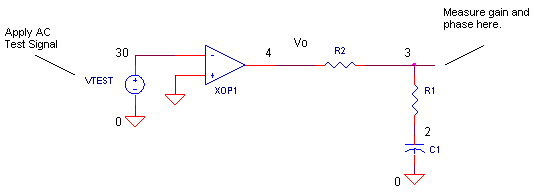
3. Apply an AC test signal VTEST where the loop was opened and observe the AC gain and phase around the loop.

The schematic above shows one way to apply open-loop analysis to the differentiator circuit. Note that breaking open the loop creates two nodes 30 and 3 where there was one.

DIFFERENTIATOR

Let's look at the open-loop circuit including the op amp modeled as basic single-pole amplifier.

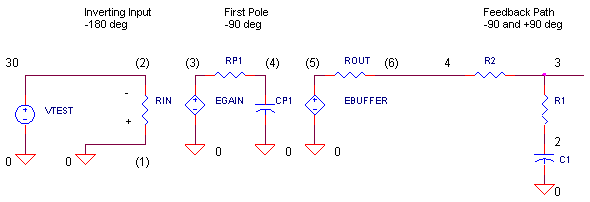
What do you notice about the feedback components when the loop is opened? Basically, R2 and C1 form a low-pass filter (pole). In a feedback amplifier, this can spell trouble by adding negative phase to overall loop, pushing the total toward -360 deg. Let's check out other phase contributors.

*Components*	*Phase Contribution*	*Comment*
Op amp Negative Input	-180 deg	A basic fact of negative feedback amplifiers. Inverting the signal results in an automatic -180 deg phase shift.
Op amp First Pole: RP1, CP1	-90 deg	A low-pass filter (pole) in the loop. Actually op amps have more poles at higher frequencies whose negative phase begin to show at lower frequencies.
Feedback Components: R2 and C1	-90 deg	R2 and C1 form another low-pass filter (pole) in the loop.
Feedback Components: R1, R2, C1	+90 deg	A zero in the loop. Finally, a positive phase contributor.

As you can see, adding up the first 3 phase contributors puts us right in the heart of oscillation territory,
-360 deg. What pulls us back to a safer phase shift? R1, of course! Let's look at the transfer function from node 4 to 3 and see what role R1 plays.

The transfer function says we can expect a pole at fp = 1/(2∙π∙C1∙(R1+R2)) contributing -90 deg of phase. However, R1 and C1 create a zero at fz = 1/(2∙π∙C1∙R1) contributing +90 of phase, shifting the total from -360 back to -270 deg, helping our mission of bringing useful and stable circuits into the world.

OPEN-LOOP TEST

Run an open-loop analysis using OPDFR_OL.CIR and plot the AC magnitude VM(3) and phase VP(3) around the loop. To get a better view, change the Y-axis of VM(3) to a log scale and plot VP(3) in a separate window.

CIRCUIT INSIGHT With R1 = 500 kΩ, C1 = 10 nF and R2 = 5 kΩ, the open-loop plots should show a stable circuit. First, find frequency where the magnitude falls to 1 V/V (or 0 dB). Now check the phase. At lower frequencies the phase drops to -360 (or 0 deg) - potential instability! (You may have noticed SPICE sometimes automatically wraps around the phases from -180, -270, -360 to +180, +90, 0 deg, respectively.)

However at high frequencies we see some good news! The phase is pulled back to about +90 deg away from 0 deg, a comfortable margin from the oscillation condition. This is all thanks to the zero created by R1 and C1. (As you might expect, nothing is for free. R1 compromises the high frequency gain of the circuit. See the Opamp Differentiator.)

Now let's remove (short) R1 and see how the circuit slips toward the edge of oscillations. Change R1 to 0.5 Ω, effectively removing it from the circuit, and run a new simulation. What's happened to the phase at the 0dB crossing? You should see the phase dangerously hugging 0 deg! The circuit would be in trouble if you closed the circuit now. Okay, let's try it! Modify the closed loop differentiator circuit OPDFR.CIR for R1 = 0.5 Ω and run a transient analysis. What does the output look like now?

SIMULATION NOTES

Check out the differentiator's closed-loop circuit.
Get a refresher of Op Amp Feedback Analysis techniques.
For a description of all op amp models, see Op Amp Models.
For a quick review of subcircuits, check out Why Use Subcircuits?
Get a crash course on SPICE simulation at SPICE Basics.
A handy reference is available at SPICE Command Summary.
Browse other circuits available from the Circuit Collection page.

SPICE FILE

Download the file or copy this netlist into a text file with the *.cir extension.

OPDFR_OL.CIR - OPAMP DIFFERENTIATOR - OPEN-LOOP ANALYSIS
*
* INPUT SOURCES SHORTED
*
C1	0	2	10NF
R1	2	3	5K
R2	3	4	500K
XOP	0 30	4	OPAMP1
*
* OPEN-LOOP TEST SIGNAL
VTEST	30	0	AC 1VAC
*
* OPAMP MACRO MODEL, SINGLE-POLE 
* connections:      non-inverting input
*                   |   inverting input
*                   |   |   output
*                   |   |   |
.SUBCKT OPAMP1      1   2   6
* INPUT IMPEDANCE
RIN	1	2	10MEG
* DCGAIN =100K AND POLE1=1/(2*PI*RP1*CP1)=100HZ
* GBP = DCGAIN X POLE1 = 10MHZ
EGAIN	3 0	1 2	100K
RP1	3	4	1000
CP1	4	0	1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER	5 0	4 0	1
ROUT	5	6	10
.ENDS
*
* ANALYSIS 
.AC 	DEC 	5 1 10MEG
*
* VIEW RESULTS
.PLOT	AC 	V(4) V(3)
.PROBE
.END

Top ↑