Op Amp Feedback Analysis
CIRCUIT
OP1.CIR (Closed-Loop Circuit) Download the SPICE file
OP1_OL.CIR (Open-Loop Circuit) Download the SPICE file
Feedback analysis is one of the most powerful tools you can wield as a designer. Why? You can optimize an amplifier or fix problems just by examining the frequency response around the feedback loop of the circuit. Suppose you’re designing a high-speed op amp to amplify a video signal. However, your amplifier overshoots and rings in response to a quick change in video level. This creates strange artifacts in the video image. What causes the overshoot and ringing? How do you fix it without degrading the bandwidth of the amplifier?
OPEN-LOOP ANALYSIS
Specifically, feedback analysis means opening up the feedback loop (Open-Loop Analysis) and observing what the gain and phase around the loop is telling you. If it’s bad news, your circuit may overshoot, ring or oscillate – these are signs of instability. What is bad news? Basically this:
If there is a frequency where the AC magnitude around the loop is 1 and the total phase is -360 or 0 deg, the circuit is unstable.
What are the consequences of instability? Closing the loop under these conditions creates an amplifier with a forward gain of infinity at this frequency – conditions for self-sustained oscillations.
OPENING THE FEEDBACK LOOP
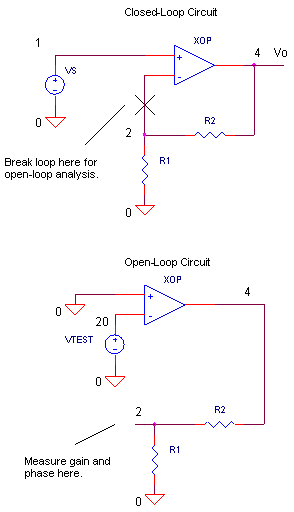
For op amp circuits, opening the feedback loop is relatively easy. Other circuits may be trickier if opening the loop changes the bias condition. To perform open-loop analysis, just follow these three steps:
1. Short the voltage source, VS.
2. Open the loop in the forward or feedback path.
3. Apply an AC test signal VTEST where the loop was opened and observe the AC gain and phase around the loop.
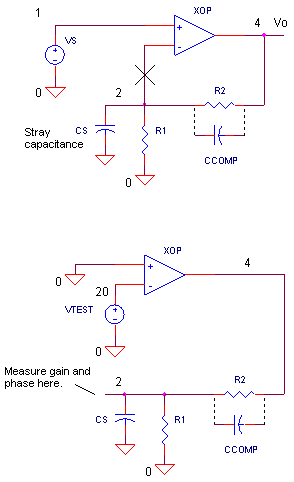
Be careful where you break the loop. Open it at a low-impedance source or a high-impedance node. By doing so, the transfer function to the opened node is essentially the same for either open or closed loop operation. For this circuit, break the loop at the op amp negative input (node 2), a high-impedance terminal. (Note that breaking the looping creates two nodes out of one ; nodes 2 and 20.) Then, apply VTEST to node 20 and check the gain and phase at node 2. Below is the open-loop circuit showing the forward path (op amp including its innards) and the feedback path (resistors).

CIRCUIT ANALYSIS Run an open-loop analysis using op1_ol.cir and plot the AC magnitude VM(2). Change the Y-axis to a log scale to get a better view. The magnitude should roll-off at low frequencies and reach a magnitude of 1 V/V (or 0 dB) at 10 MHz.
The phase is a little more interesting. Plot the phase VP(2). You may have to add a new plot to get a good view. Check out how it starts off already at -180 deg (or +180 deg if your plotter automatically wraps it around to a positive scale for you.) Why? The negative input of the op amp inverts the signal producing -180 deg of phase right out of the gate. But wait, there more phase to be subtracted! The op amp’s single pole CP1 and RP1, contributes an additional -90 deg for a total of -180 -90 = -270 deg (or +90 deg). Is this circuit stable or unstable? The answer is a stable one because the phase VP(2) is nowhere near -360 deg (or 0 deg) at the frequency where the magnitude VM(2) crosses 1.
THE ULTIMATE TEST – THE STEP RESPONSE
Pass the bubbly, you’ve performed your first stability analysis. The circuit looks stable, but, how do you put the amplifier to a real test? Just close the loop, apply a step function to the input and watch the output behavior.
CIRCUIT ANALYSIS Run a simulation using the op1.cir circuit, the closed-loop version of op1_ol.cir. Plot the input V(1) and output V(4). The transient response for a stable amplifier should reach its final value with little overshoot or ringing.
TROUBLE AHEAD – STRAY CAPACITANCE
Here’s a chance to stare directly into the face of a real world situation that can make the output of your amplifier jump and buck like a wild stallion. Let’s find out the cause and how to tame it.
CIRCUIT INSIGHT Electronic circuit boards can add a significant amount of stray capacitance to a pair of nodes. Add CS=10pF across R1 in the op1.cir file by removing the * at the beginning of the CS 2 0 10PF device statement.
Simulate the circuit. What happened to the step response at the V(4)? This ringing and overshoot may be unacceptable for a video or high-speed data-acquisition system!
How do you fix it? Open up the loop and let’s see the effect of CS on the gain and phase. Add CS = 10 pF across R1 in the open-loop circuit file op1_ol.cir (remove the * before the CS statement). Run a simulation and plot the AC magnitude VM(2) and the phase VP(2). What’s happened to the phase? CS creates a low-pass filter with R1. This contributes another -90 deg to the -270 deg phase for a total near -360 (or 0 deg) at the frequency where the magnitude crosses 1. And the closer the phase approaches -360 (or 0 deg), the more unstable your circuit becomes.
THE FIX – THE COMPENSATION CAP
The fix is easy. If CS creates a low-pass filter with R2 (subtracts phase from the loop), then, simply add capacitor CCOMP to create a high-pass filter with R1 (adds phase to the loop). The right CCOMP will cancel the effect of CS. How do you know which value of CCOMP to choose? Just pick CCOMP such that R1 x CS = R2 x CCOMP.
HANDS-ON DESIGN Rescue this circuit by adding CCOMP. (Example: CCOMP = [R1 x CS] / R2 = 10pF) Add CCOMP across R2 by removing the * at the beginning of the CCOMP device statement. Run the open-loop circuit and plot the magnitude VM(2) and phase VP(2). Does the phase reach -360 (or 0) deg as before? The phase should behave as if CS were not there reaching only -270 (or +90) deg.
Of course, the final test is the step response of the closed-loop circuit. Add CCOMP across R2 in the op1.cir circuit file. Try out the circuit. Where there was once wild overshoot and ringing at V(4), there should be a tamed response. You’ve successfully rescued your amplifier with feedback analysis in your toolkit.
OSCILLATOR DESIGN
Feedback analysis helps us design amplifiers without inadvertently creating oscillators. But what tool do we use to design oscillators on purpose? As you might have guessed, the same feedback analysis tool. See the design of an Wien-Bridge oscillator.
SPICE FILES
Download the file or copy this netlist into a text file with the *.cir extention.
OP1_OL.CIR - OPAMP OPEN-LOOP FEEDBACK ANALYSIS * VTEST 20 0 AC 1 * XOP 0 20 4 OPAMP1 R1 2 0 10K * CS 2 0 10PF R2 2 4 10K * CCOMP 2 4 10PF * * OPAMP MACRO MODEL, SINGLE-POLE * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) EGAIN 3 0 1 2 100K RP1 3 4 1K CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * ANALYSIS .AC DEC 10 10 100MEG * * VIEW RESULTS .PRINT AC VDB(2) VP(2) .PLOT AC VDB(2) VP(2) .PROBE .END
Download the file or copy this netlist into a text file with the *.cir extention.
OP1.CIR - OPAMP CLOSED-LOOP STEP RESPONSE * STEP INPUT VS 1 0 AC 1 PWL(0US 0V 0.1US 1V 10US 1V) * R1 2 0 10K * CS 2 0 10PF R2 2 4 10K *CCOMP 2 4 10PF XOP 1 2 4 OPAMP1 * * SINGLE-POLE OPERATIONAL AMPLIFIER MACRO-MODEL * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) EGAIN 3 0 1 2 100K RP1 3 4 1K CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * ANALYSIS .AC DEC 10 10 10MEG .TRAN 0.01US 1US * * VIEW RESULTS .PRINT AC VM(4) .PLOT AC VM(4) .PLOT TRAN V(1) V(4) .PRINT TRAN V(1) V(4) .PROBE .END
© 2002 eCircuit Center