About SPICE | SPICE Basics | Running SPICE | CIRCUIT COLLECTION | SPICE Commands | SPICE Demos and Downloads
About Us | Contact Us | Home | Search
 

Op Amp
Gain Resistor Errors
 

CIRCUIT

       R1 + ΔR1                  R2 + ΔR2

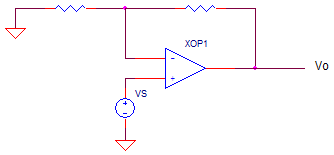
                                  OP_GAIN_R_ERR1.CIR                Download the SPICE file

The good news about op amp design is that the gain is largely dependent on the ratio of external resistors R2 and R1. This greatly simplifies amplifier design! Unfortunately, most of the burden for gain accuracy falls on the accuracy of R1 and R2. What if your product design calls for a sensor preamp that's 2% accurate over a temperature range of 25 deg C +/-20 deg C? What resistor tolerance (TOL) and temperature coefficient (TC) do you choose to meet your design goals?

RESISTOR ERRORS

From your design calculations, you find your target resistor values R1 and R2. However, none of the resistors delivered to your door will be the exact value ordered. The actual resistor can be modeled as the ideal value plus a resistance error.

R1 + ΔR1
R2 + ΔR2

The errors ΔR1 and ΔR2 are usually broken up into two types of errors: Tolerance and Tempco

Initial Tolerance (TOL) in %

ΔR1 = R1 ∙ TOL / 100
ΔR2 = R2 ∙ TOL / 100

Temperature Coefficient (TC) in ppm / C

ΔR1 = R1 ∙ TC/1e6 ∙ ΔT
ΔR2 = R2 ∙ TC/1e6 ∙ ΔT

Turns out that resistors change their value quite linearly with temperature. The amount of change per degree C is typically so small its units are in a ratio of parts per million or ppm/C.

Also, the error term ΔR1 and ΔR2 can be in either direction - positive or negative.

NON-INVERTING GAIN ERROR

So how does the resistor error effect non-inverting gain accuracy? A simple method involves some straightforward calculations. Just calculate the ideal gain K, the gain with resistor error K' and then calculate the percent error.

Kerr =  (K' - K) / K · 100%

RESISTOR TOLERANCE (TOL)

For R1 = 1000 Ω, R2 = 1000 Ω, what is gain error for TOL = 1% ?

First we ask, how much resistance error is 1%?

ΔR1 = R1 · TOL = 1000 · 1/100 = 10 Ω
ΔR2 = R2 · TOL = 1000 · 1/100 = 10 Ω

Then, how does ΔR1 affect the gain?

Finally, what is % gain error due to R1?

Similarly, how does R2 affect the gain?

What is the % gain error due to R2?

What is the total error? You can calculate the worst case error the adding the absolute values of the individual errors.

Kerr_tot = |Kerr_R1_TOL| + |Kerr_R2_TOL|
              = | -0.5% |   +   | +0.5% |
              = 1%

Why add absolute values? Because the actual resistor TOL of 1% is actually ±1%; the error can be either positive and negative direction! You can see that adding the errors directly would result in Kerr_tot = -0.5%  +  +0.5% = 0%. This happy result happens only if the resistor errors are in the same direction - not a solid design assumption.

RESISTOR TEMPERATURE COEFFICIENT (TC)

What is gain error for TC = 200 ppm/C over a temperature change of  ΔT = 20 C ?

What are the the resistance errors due to the tempco?

ΔR1 =    R1      ∙    TC  ∙  ΔT
        = 1000 Ω  ∙  200/10⁶ /C  ∙  20 °C
        =  4 Ω

ΔR2 =    R2      ∙   TC   ∙  ΔT
        = 1000 Ω  ∙  200/10⁶ /C  ∙  20 °C
        =  4 Ω

Now calculate the gain error, just like we did for the tolerance error above.

Kerr_R1_TC = -0.2%

Kerr_R2_TC = +0.2%

Finally, add all of the errors

Kerr_tot = | Kerr_R1_TOL | + | Kerr_R2_TOL | + | Kerr_R1_TC |   + | Kerr_R2_TC |
              =  | -0.5%| + | +0.5% | + | -0.2% |   + | +0.2% |
              =  1.4%

Did we meet out initial goal of 2% over a temperature swing of ΔT = +/-20 C? Awesome news! But what if Kerr_tot > 2%, what then? We must go back to the manufacturer's catalog and search for a resistor with a smaller TOL and/or TC.

INVERTING GAIN ERROR

Now, how can you apply the same error analysis to the inverting amplifier? Just calculate the errors due to ΔR1 and ΔR2 using the ideal gain equation K =  - R2 / R1.

In fact, using this method you can calculate the error of any amplifier configuration via its gain equation. How about a differential amplifier with four resistors - R1, R2, R3 and R4? You guessed it - find the errors due to ΔR1, ΔR2, ΔR3 and ΔR4. Yes, it's a lot of number crunching, but that's what spreadsheets are for.

SIMULATION

Let's simulate the non-inverting amp with ideal resistor values R1 = 1000 and R2 = 1000 for a gain of +2.. With the input signal at VS=1V, we expect to see the output voltage represent the gain
V(4) = VS * (R2/R1+1) = 2.

 CIRCUIT INSIGHT    Run a Transient Simulation and plot the output V(4). Place a cursor on the trace to get a precise reading of the output voltage. Is should be very close to 2.00. Now, add ΔR1 to R1 that represents an error due to 1% tolerance, 1000 + 10 =  1010. Set R1 to this new value and rerun the simulation. Did the gain reduce to 1.99 as calculated above?

Now also set R2=1010 to mimic the same 1% error. What happens to the gain? Are you surprised that the gain is back to 2.00? That's because the gain depends on the ratio of resistors. If R1 and R2 both rise by the same amount, then the ratio stays the same, and so does the gain.

What happens if ΔR1 and ΔR2 are in opposite directions. Set R2=1000+10=1010 and
R1=1000-10=990. Now run a simulation and check the gain. Did the gain rise to 2.02 (1% total error) as calculated above due to TOL only.

Finally let's simulate the worst case error due to both TOL and TC. Set R2=1000+10+4=1014
and R1=1000-10-4=986. What is the total error expected? An error of 1.4% should result in a gain
of 2.00 * 1.014 = 2.028. What if the resistor errors were in the opposite direction?
Set R2=1000-10-4=986 and R1=1000+10+4=1014. What happens to the gain?

 HANDS-ON DESIGN    Suppose your original design goal was a maximum error of 0.25% over a temperature change of ΔT = +/-20 C. You have the budget to buy resistors with TOL=0.1%. But which TC to you choose: 200, 100, 50 or 25 ppm/C?

ALTERNATE METHODS

When is comes to calculating gain errors, there's more than one way to fillet this fish. You can calculate component sensitivities do some calculus on the equations to find the sensitivities. Or you can let SPICE calculate the component sensitivities for you. For more, see the topics Component Tolerances Part 1 and Part 2.

SPICE FILE

Download the file or copy this netlist into a text file with the *.cir extension.

OP_GAIN_RES.CIR - OP AMP WITH GAIN RESISTOR ERRORS
*
* INPUT VOLTAGE
VS	3	0	DC	1.0V
*
* GAIN RESISTORS WITH ERRORS
*
R1	0	2	1000
R2	2	4	1000
XOP1	3 2	4	OPAMP1
*
*
* OPAMP MACRO MODEL, SINGLE-POLE
* connections:      non-inverting input
*                   |   inverting input
*                   |   |   output
*                   |   |   |
.SUBCKT OPAMP1      1   2   6
* INPUT IMPEDANCE
RIN	1	2	10MEG
* GAIN BW PRODUCT = 10MHZ
* DC GAIN (100K) AND POLE 1 (100HZ)
EGAIN	3 0	1 2	100K
RP1	3	4	1K
CP1	4	0	1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER	5 0	4 0	1
ROUT	5	6	10
.ENDS
*
* ANALYSIS 
.TRAN 	0.1MS  10MS
.PROBE
.END

Top ↑

© 2010 eCircuit Center