COMPONENT TOLERANCES AND
TEMPCOS
PART II
CIRCUIT
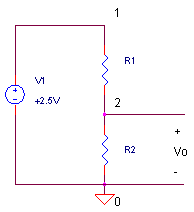
R_DIVIDER.CIR Download the SPICE file
In Part I, we've found out how much our DC voltage Vo changes given a change in R1 and R2. How did we do it? Method I used your basic plug and chug method of manually changing resistor values by small amounts, and in various directions and combinations, to see how it changes the divider voltage. Methods 2 and 3, will show us more elegant and efficient ways to answer the same question.
METHOD 2 - DERIVATIVES
In calculus, the derivative is the perfect tool for the job at hand. The derivative shows us by an equation, how one variable (V1) changes given a change in some other variable (R1 or R2). So given the equation for a voltage divider
Vo = V1 ∙ R2 / (R1 + R2)
we take the derivative of Vo with respect to R1 and R2 to get
dVo⁄dR1 = d⁄dR1 ( V1∙ R2 / (R1 + R2) )
= - V1∙ R2 / (R1 + R2) 2dVo⁄dR2 = d⁄dR2 ( V1∙ R2 / (R1 + R2) )
= + V1∙ R1 / (R1 + R2) 2
The units of the this derivative are in V per Ω. ( Take heart, my calculus tools show signs of rust too. See refresher below.)
Okay, plugging some real numbers into these equations, R1 = 1500 Ω, R2 = 1000 Ω and V1 = +2.5V, let's calculate the derivatives. Then we'll compare these numbers to the ones calculated by hand in Part I.
dVo⁄dR1 = - 2.5V ∙ 1000 Ω / (1000 Ω + 1500 Ω) 2
= -0.0004 V/Ω
dVo⁄dR2 = 2.5V ∙ 1500 Ω / (1000 Ω + 1500 Ω) 2
= 0.0006 V/Ω
Good news - these values match the ones calculated manually in Method 1. So what do these derivatives tell us? Basically, if R1 changes by 1 Ω, expect Vo to change by -0.4 mV. Likewise, if R2 changes by the 1 Ω, expect Vo to change by +0.6 mV.
Now the voltage change over the total resistance change is easily calculated as
ΔVo = dVo⁄dR1 ∙ ΔR1
ΔVo = dVo⁄dR2 ∙ ΔR2
As an example, suppose you've bought 1% resistors, how much will Vo change when R1 or R2 are 1% above their nominal value?
ΔR1 = R1 ∙ TOL = 1500 Ω ∙ 0.01 = 15 Ω
ΔR2 = R2 ∙ TOL = 1000 Ω ∙ 0.01 = 10 Ω
Consequently, how much will Vo change?
ΔVo = dVo⁄dR1 ∙ ΔR1
= -0.0004 V/Ω ∙ 15 Ω
= -0.006 V
ΔVo = dVo⁄dR2 ∙ ΔR2
= 0.0006 V/Ω ∙ 10 Ω
= +0.006 V
Interesting! A 1% change in either resistor caused the same magnitude of voltage error, even though the resistor values are different.
METHOD 3 - THE POWER OF SPICE
The creators of SPICE added a powerful capability to their algorithms - DC Sensitivity. Just include
.SENS <output1> <output2> ...
in your netlist. After the BIAS point calculation, SPICE determines the sensitivity of each output to all of the components (resistors, transistors, etc) in your circuit.
CIRCUIT INSIGHT Okay, we'll let SPICE do some work for us. Add the statement
.SENS V(2)
to the R_DIVIDER.CIR circuit file and run a
simulation. Open the *.OUT file let's see if SPICE agrees with our previous
methods of sensitivity calculations. Well, shoot my horse and paint me red,
the results in the column labeled "Element Sensitivity" matches our previous
values of dVo⁄dR1
and
dVo⁄dR2.
DC SENSITIVITIES OF OUTPUT V(2)
ELEMENT ELEMENT ELEMENT NORMALIZED
NAME VALUE SENSITIVITY SENSITIVITY
(VOLTS/UNIT) (VOLTS/PERCENT)
R1 1.500E+03 -4.000E-04 -6.000E-03
R2 1.000E+03 6.000E-04 6.000E-03
V1 2.500E+00 4.000E-01 1.000E-02
Also, SPICE adds a bonus column labeled "Normalized Sensitivity" in VOLTS/PERCENT. Why? This can save you a step of calculations by estimating your circuit errors based on percent of error instead of units like ohms. SPICE even calculated the sensitivity of Vo to V1.
Now, let's find the error from our 1% resistors where ΔR1 = R1 ∙ TOL = 1500 Ω ∙ 0.01 = 15 Ω and ΔR2 = R2 ∙ TOL = 1000 Ω ∙ 0.01 = 10 Ω. Using SPICE's sensitivities we get
ΔVo = dVo⁄dR1 ∙ ΔR1
= -4.000E-4 V/Ω ∙ 15 Ω
= -0.006 V
ΔVo = dVo⁄dR2 ∙ ΔR2
= 6.000E-4 V/Ω ∙ 10 Ω
= +0.006 V
which is the same results as Methods 1 and 2.
Although this was a simple example, the real payoff comes from letting SPICE calculate sensitivities for larger circuits. You can imagine the difficulty in calculating derivatives for 20 to 30 components in a complex network.
So how can you use the results of the .SENS statement? One way is by loading the results into an Excel spreadsheet. Then, by first calculating component changes based on tolerances and tempcos, you can calculate the output's initial error and temperature drift due to each component.
CIRCUIT INSIGHT Question! Suppose a resistor divider produces a voltage closer to 1 V or 0 V. Does Vo get more or less sensitive to resistor changes? Run a simulation with values like R1 = 1 kΩ and R2 = 9 kΩ. Then flip the values to R1= 9 kΩ and R2 = 1 kΩ. What happens to the sensitivities compared to the original case with similar values of R1 and R2 that produced mid-range voltages like Vo = 1.0 V?
TOTAL ERROR
How do you find the total error from all components? First, we realize that a 1% tolerance really means +/-1% error maximum. Depending on the sign, the effect of two or more resistors could either cancel or add to each other. If performing worst case analysis, you assume the worst (of course) and add the absolute value of all the errors.
ΔVo_tot = | dVo⁄dR1 ∙ ΔR1 | + | dVo⁄dR2 ∙ ΔR2 | + ...
CALCULUS REFRESHER
You say your math power tools need tuning up? I searched web using keywords like "calculus refresher" to find a number of much needed re-primers for myself such as this one.
Let me know if you find other goodies out there! To find the derivative of the resistor divider equation, we use the derivative of powers
d⁄dt t n = n t n − 1 for any n ≠ 0
and the product rule
d⁄dt (h(t) × g(t)) = h×g' + h'×g
By setting up the divider equation to look like this
Vo = V1∙ R2 ∙ (R1 + R2)-1
the derivatives can be found from these starting points
dVo⁄dR1 = d⁄dR1 ( V1∙ R2 ∙ (R1 + R2)-1 )
dVo⁄dR2 = d⁄dR2 ( V1∙ R2 ∙ (R1 + R2)-1 )
= V1∙ R2 ∙ d⁄dR2( (R1 + R2)-1 ) + d⁄dR2(V1∙ R2) ∙ (R1 + R2)-1
(No point in showing the whole derivation. It was satisfying for me to work and finally find the answer - wouldn't want to spoil it for you.)
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
R_DIVIDER.CIR - FIND COMPONENT SENSITIVITY * V1 1 0 DC 2.5V R1 1 2 1500 R2 2 0 1000 * * ANALYSIS .TRAN 1MS 10MS .SENS V(2) * * VIEW RESULTS .PROBE .END
© 2005 eCircuit Center