Op Amp All-Pass Filter
CIRCUIT
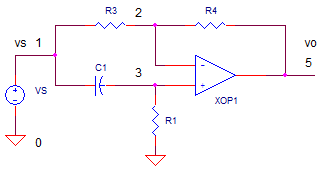
OP_ALL-PASS1.CR Download the SPICE file
The All-Pass Filter went largely ignored by me for many years until I ran into it studying a guitar effect pedal, the phase-shifter. The heart of this popular effect pedal is an all-pass filter that creates a time delay of the guitar signal. The delay acts as the key block of a comb filter - multiple notch filters. So I figured the door had opened to learn about this circuit.
ALL-PASS WITH DELAY
The "all-pass" part of this filter refers to unity-gain across the
across all frequencies.
However, it's the phase (or time-delay) that varies across a frequency
band.
Basically, the magnitude of the gain remains at unity while the
unity gain changes slowly from an inverting configuration (180 deg) to a non-inverting
gain (0 deg) over the frequency band.
Where is the transition between inverting and non-inverting behaviors? The corner frequency is defined by
fc = 1/ ( 2 pi R1 C1)
The table below summarizes the all-pass action.
| Frequency | Config | Phase | Delay of sine-wave | Comment | |
| f << fc | Inverting | -180 deg | Half cycle | C1 is open, signal passes through inverting path. | |
| f = fc | na | -90 deg | Quarter cycle | C1 begins to look like a short, passing significant signal through the positive path. | |
| f >> fc | Non-Inverting | 0 deg | None | C1 is shorted, allowing only the non-inverting behavior. |
TRANSFER FUNCTION
How can you find the transfer function? Simply unhook the two
inputs and analyze each path separately. The negative input looks like
the standard inverting amplifier.
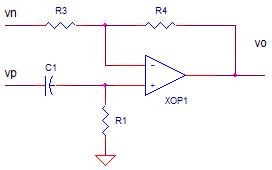
The positive path looks like a high pass filter R1,C1 followed by a non-inverting gain defined by R4 and R3.
vop = vn · -R4/R3 vop = vp · R1/(R1+1/(sC1)) · (1+R4/R3)
Finally, tie the inputs together (vn=vp=vs), set R4/R3 = 1 and add the outputs together.
vo = vop + von
= vs · R1/(R1+1/(s·C1)) · 2 - vs
After getting a common denominator, some simplifying, labor pains and ultimately joy, you get
vo/vs = ( 1 - s·R1·C1 ) / ( 1 + s·R1·C1 )
The magnitude and phase look like this
Mag = 1 Phase = -tan (2 pi f R1 C1) + tan ( -2 pi f R1 C1 )
What story is this telling us? Across the frequency range, it has unity
gain. But, the phase starts out at
-180 deg (1/2 wave delay) at frequencies
below fc and ends up at 0 deg (0 delay) above fc.
FREQUENCY RESPONSE
Run an AC ANALYSIS of OP_AL_PASS1.CIR and plot the input V(1) and
output V(5). Setting R1=10k and C1=0.1uF, we calculate fc =
1/(2·pi·10k·0.1uF = 159 Hz.
CIRCUIT INSIGHT Does the magnitude hold steady at 1 across the frequency range? Does the phase reach -180, -90, and 0 when the frequency is below, at, and above fc?
Eventually at 1MHz the output drops. Why? What is the Gain Bandwidth Product
of the op amp model?
TRANSIENT RESPONSE
Now let's relate the
phase delay of the filter plots to the actual time delay. Voltage
source VS creates a sine wave to help you see the time delay. SPICE lets you
set a parameter used in the simulation. For this example, set a variable fo
to check the filter's delay at frequencies below and above fc.
.PARAM fo=1.6Hz
The variable fo also sets the length of simulation time
.TRAN 0.1MS {4/fo}
to conveniently include several sine cycles. Nice feature - less monkeying with the setup at each run.
CIRCUIT INSIGHT Initially, set fo=1.6 Hz, one hundred times below fc=159 Hz. Run a TRANSIENT ANALYSIS of OP_ALL_PASS1.CIR and plot the input and output V(5). What is the expected output? Is the output delayed by 1/2 cycle (a.k.a. -180 deg or inverting)?
Rerun the simulation with fo=16 Hz, 160 Hz, 1600Hz and 16000Hz. Does the time delay through the filter progressively shift as the frequency increases? Cool beans - the time delay changes (phase shift), yet the magnitude stays the same!
CASCADED FILTERS
CIRCUIT INSIGHT
How can you get twice the phase shift? You may have noticed
another filter stage in the SPICE file. Simply rerun OP_ALL_PASS1.CIR and plot
the output at V(25). What is the delay of the sine wave from as the
frequency of the sine is stepped from 1.6Hz to 16kHz
through two filter stages?
UPCOMING TOPIC
The all-pass filter lies at the heart of the
Phase Shifter, an audio effects pedal
that creates a swirling sound used widely rock and pop music. Essentially,
the effect creates a comb filter (multiple notches) whose frequencies are
slowly swept back and forth. The all-pass is a key element in creating a
notch filter. It's simpler than I thought.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
* op_all-pass1.cir
*
.PARAM fo=1.6Hz
VS 1 0 AC 1 SIN(0V 1V {fo})
*
C1 1 3 0.1UF
R1 3 0 10k
R3 1 2 10K
R4 2 5 10K
XOP1 3 2 5 OPAMP1
*
C21 5 23 0.1UF
R21 23 0 10k
R23 15 22 10K
R24 22 25 10K
XOP2 23 22 25 OPAMP1
*
*
* OPAMP MACRO MODEL, SINGLE-POLE
* connections: non-inverting input
* | inverting input
* | | output
* | | |
.SUBCKT OPAMP1 1 2 6
* INPUT IMPEDANCE
RIN 1 2 10MEG
* GAIN BW PRODUCT = 10MHZ
* DC GAIN (1MEG) AND POLE 1 (10HZ)
EGAIN 3 0 1 2 1000K
RP1 3 4 1K
CP1 4 0 15.9UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER 5 0 4 0 1
ROUT 5 6 10
.ENDS
*
* ANALYSIS *************************************
.TRAN 0.1MS {4/fo}
*.TRAN 10MS 5S
*.ac dec 40 1 1000k
.PROBE
.END
© 2012 eCircuit Center