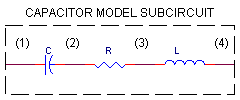
Capacitor Model
CIRCUIT
CMODEL1.CIR Download the SPICE file
Ideal capacitors exist only in textbooks, not on real circuit boards. You
may be surprised to find that all
practical capacitors look (behave) similarly to the series RLC network shown above.
Whether you're designing a filter or picking bypass capacitors, you'll need to
know what your capacitor looks like across the entire frequency range. As you can
imagine, having inductance in your filter at high frequencies where
your intent was a capacitor, can produce some unexpected results.
REAL CAPACITORS
The reality of producing capacitors creates two parasitic components that come along with the package: inductance and resistance. External leads and internal paths create inductive and resistive parasitic components. So how does the real capacitor behave versus frequency? You can break down the behavior into three frequencies.
frequency
impedance
Low Capacitive
Self-Resonance Resistive
High Inductive
At low frequencies, the capacitor's impedance looks just like you'd expect from the specified capacitor value. At self-resonance, the capacitive and inductive impedances cancel each other out leaving only a resistive component. The self resonance is given by
![]()
The resistive component is usually referred to as the Equivalent Series Resistor (ESR). Above self-resonance, the inductive reactance takes over as it grows much larger than the capacitive reactance and ESR.
CAPACITOR SPICE MODEL
What values of C, L and R do you choose to create the capacitor model? The table below shows you how to assign values.
| component | value | |
| C | Capacitance | |
| R | ESR | |
| L | L = 1/ [( 2π
fo)²
x C] where fo is the self-resonant frequency |
The capacitance value comes right from its specified value. The ESR and self-resonant frequency fo are usually available from the manufacturer's web site or by request.
Let's create capacitor models for 1 uF and 0.1 uF capacitors. For a 1 uF capacitor, ESR = 0.03 ohms, fo = 1 MHz and we calculate L = 25.3 nH. Similarly, for the 0.1 uF capacitor, ESR = 0.08 ohms, fo = 10 MHz and we calculate L = 2.53 nH.
It's convenient to create a subcircuit for the three elements of the capacitor. Why? This makes it easy to insert the model into a new or existing circuit. (See Why Use Subcircuits?) For the 1 uF capacitor, the subcircuit call and definition are shown below.
XC1 1 0 C105 ;subcircuit inserted at nodes 1 and 0
.SUBCKT C105 1 4 ;subcircuit definition
* FO = 1 MHZ
C 1 2 1UF
R 2 3 0.03OHMS
L 3 4 25.3NH
.ENDS
CAPACITOR IMPEDANCE VS FREQUENCY
How do you plot the impedance of a network? One trick is to drive the network with a 1A RMS current source and then plot the voltage across the network. This works because the voltage is equal to the impedance under these conditions ( V = Z x I = Z x 1 = Z).
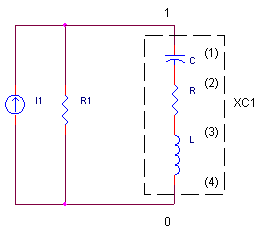
CIRCUIT INSIGHT Run a simulation of the SPICE file CMODEL1.CIR. Look at the the impedance of the 1 uF model (C105) by plotting VM(1). Change the Y-axis to a log scale to get a better view. If this were an ideal capacitor, what would you see? The impedance would get smaller as frequency increases Xc = 1/(2π x C x f). However, the impedance of this model takes a dip at self-resonance and then starts increasing with frequency! The inductive impedance takes over (Xl = 2π x L x f ) . This may produce disappointing results if this capacitor is chosen for a filter operating at frequencies near or above its self-resonance.
How do we know the impedance is capacitive and inductive at frequencies
below and above self-resonance? Plot the phase shift of the network by
adding a new plot window and adding trace VP(1). Negative and positive phase
indicate capacitive and inductive reactances, respectively.
IMPEDANCE VS. CAPACITOR SIZE
CIRCUIT INSIGHT
For a given capacitor type, what happens to the self-resonant
frequency for smaller capacitor values? Plot the impedance of a 0.1uF
capacitor (C104) by adding trace VM(2). The self-resonance is higher making
this capacitor more useful at higher frequencies. To see these models in
action, check out Power Supply Bypassing.
CAPACITOR NOTES
These subcircuits model a capacitor's self-resonant and series resistive
behavior. More complex models can be created that mimic other non-ideal
behaviors such as dielectric absorption, leakage and temperature effects.
Some capacitor manufacturers provide SPICE models that include
these effects.
SPICE MODEL CALCULATOR
Check out this handy webpage that creates a
capacitor SPICE model.
Simply enter the essential parameters and the JavaScript/HTML code spits out
a subcircuit for you to copy into your netlist or SPICE library file.
SIMULATION NOTE
You may have noticed R1 = 100MEG to ground across the capacitor model. What's the purpose of this component if it has little effect on the impedance? The problem is that without R1, node 1 has no resistive path to ground; SPICE is not happy under these conditions and may grind to a halt. The 100MEG resistor solves the problem by providing a DC path to ground.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extention.
CMODEL.CIR - CAPACITOR MODEL * * MEASURE IMPEDANCE OF CAPACITORS USING 1A CURRENT SOURCES I1 0 1 AC 1 XC1 1 0 C105 R1 1 0 100MEG * I2 0 2 AC 1 XC2 2 0 C104 R2 2 0 100MEG * * 1 UF CAPACITOR MODEL - INCLUDES ESR AND SELF-RESONANCE .SUBCKT C105 1 4 * FO = 1 MEG HZ C 1 2 1UF R 2 3 0.03OHMS L 3 4 25.3NH .ENDS * * 0.1 UF CAPACITOR MODEL - INCLUDES ESR AND SELF-RESONANCE .SUBCKT C104 1 4 * FO = 10 MHZ C 1 2 0.1UF R 2 3 0.08OHMS L 3 4 2.53NH .ENDS * * ANALYSIS .AC DEC 40 10K 100MEG * VIEW RESULTS .PRINT AC VM(1) VP(1) .PLOT AC VM(1) VP(1) .PROBE .END
© 2002, 2014 eCircuit Center