Op Amp Model

About SPICE | SPICE Basics | Running SPICE | CIRCUIT COLLECTION | SPICE Commands | SPICE Demos and Downloads
About Us | Contact Us | Home | Search
 

Slew-Rate Using TANH

CIRCUIT

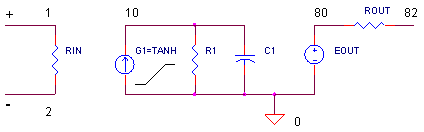
IG1 = I1*TANH(K1*V(1,2))

                                          OP_TANH_SLEW.CIR   Download the SPICE file

Slew-rate defines the speed limit of how fast the op amp's output voltage can change. Many op amp models use a transistor differential input stage because it closely resembles the actual input stage. While useful, they require many components and can be cumbersome to calculate. Also, this complex model can make for long simulation times or convergence problems. But, there's a simpler solution available - one that models the same gain, bandwidth and max slew-rate behavior with only a few components. We go to the Analog Behavioral Modeling toolshed and fire up the TANH function (hyperbolic tangent). 

DIFFERENTIAL INPUT STAGE

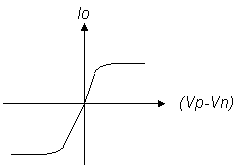
How does the hyperbolic tangent (TANH) function help model slew rate behavior? Its transfer function approximates a transistor differential input stage via two desirable features.

    ►  For small input signals (Vp - Vn), the output current is linear.                           Io = K * (Vp - Vn)
    ►  For large input signals, Io has a max value equal to the stage's bias current I1.  Io_max = I1

The transfer function has a slope of K = Io / (Vp-Vn) and a max current of  I1.

And its this max output current I1 charging up capacitance C1, that produces an output voltage ramp. This ramp defines the max dV/dt (voltage rate of change), or slew-rate, of the op amp.

                                            dV /dt max = slew rate = I1 / C1

HYPERBOLIC TANGENT

In its simplest form, the hyperbolic tangent looks like this

              Function                 y = tanh( x )
              For small x             y = x
              For large x              y = 1                            

To make it work in our op amp model, let's modify it a bit. This modified function defines the output from current source G1.

              Function                 Io = I1 · tanh( K1 · (Vp - Vn ) )
              For small inputs      Io = I1 · K1 · ( Vp - Vn )
              For large inputs       Io = I1  

SPICE MODEL

The SPICE model looks much like the Basic Op Amp Model. Just three components - G1, R1 and C1 - models open-loop gain, bandwidth and slew rate. Here's an example netlist.

G1   100   10    VALUE = { 0.01*TANH(3.142*V(1,2)) }
R1   10    100   3.183e+007
C1   10    100   5e-010

How do calculate these components? Suppose you need to model an op amp with the following specs.

Open-Loop Gain          1,000,000 V/V
Unity Gain Bandwidth  10 MHz
Slew Rate                   20 V/us

A few simple calculations get you there. First, choose I1.

          I1 = 10 mA

Next, calculate C1 to achieve your slew rate.

          C1 = I1 / Slew

Now, to take care of the bandwidth we need to know the location of the pole fp1. Then, using C1  calculate R1 to make it happen.

          fp1 = fu / Aol
          R1 = 1 /(2 · pi · fp1 · C1)

Finally, the output voltage is produced by G1's current

          I1*TANH(K1*V(1,2))

working into R1. For small V(1,2), the output is  V(10) = IG1·R1 = I1·K1·V(1,2)·R1. Or you can write,

                    Aol  = V(10) / V(1,2)  =  I1 ·  K1 · R1.

Simply solve for K1 and calculate it.

          K1 = Aol / (I1 * R1)

For our example, let's crunch the numbers.

ROAD TEST

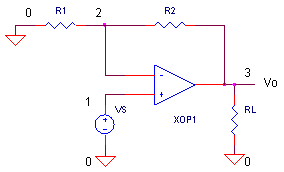
To test drive our op amp model, we'll use the non-inverting amplifier

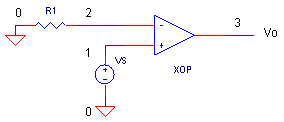
 OPEN-LOOP AC RESPONSE   To open the loop, remove R2 by placing a "*" in front of the R2 statement. R1 = 10 kΩ grounds the negative input. 

Run an AC Analysis and plot the output V(3). How does the SPICE model perform? Does the open-loop response show a gain at low frequencies of Aol = 1e6 V/V? See if the gain falls to 0.707 of max amplitude at fp1 = 10 Hz. To get a better view, change the Y-Axis Settings to a log scale. And finally, does V(3) drop to unity at fu = 10 MHz? So far so good! Now let's check the slew rate.

 CLOSED-LOOP RESPONSE   Replace R2 into the circuit by removing the "*" at the beginning of the statement. VS generates a 5 V square wave. Run a Transient Analysis and plot the input V(1) and output V(3). With R1 = R2 = 10 kΩ, the non-inverting gain is 2 V/V. For a 5 V input, how fast does the output reach 10 V? For a slew-rate of 20 V/μs, you should get to 10 V in 0.5 μs.

Increase the gain by increasing the R2 / R1 ratio. Can you estimate the output voltage? More importantly, can you predict how long it will take your amplifier to reach it?

 CIRCUIT INSIGHT   During the slew-rate limited interval, check the peak current from G1 by plotting
I(XOP1.G1). As advertised, it should max out at 10 mA. This is the max juice available to charge C1.

SIMULATION NOTES

For a description of all op amp models, see Op Amp Models.
For a quick review of subcircuits, check out Why Use Subcircuits?
Get a crash course on SPICE simulation at SPICE Basics.
A handy reference is available at SPICE Command Summary.
This op amp model can be used for many of the op amp circuits available from the Circuit Collection page.

SPICE FILES

Download the file or copy this netlist into a text file with the *.cir extension.

OPAMP_TANH.CIR
*
* SIGNAL SOURCE
VS 1 0	AC 1	PWL(0US 0V   0.01US 5V  2US 5V   2.01US -5V  4US -5V)

* NON INVERTING
R1	0	2	10K
R2	2	3	10K
XOP1	1  2    3       OP_TANH1
RL	3	0	100K

* OP AMP MODEL - TANH *************************
*                       In+  In-  Vout
.SUBCKT OP_TANH1	1    2    82
*
* INPUT R
RIN	1	2	1000MEG
*
*  INPUT STAGE: GAIN, POLE, SLEW
G1	0	10	VALUE = {  0.01*TANH(3.142*V(1,2)) }
R1	10	0	3.183e+007
C1	10	0	5e-010
*
* OUTPUT STAGE
EOUT	80 0	10 0	1
ROUT	80	82	10
.ENDS
*
* ANALYSIS ************************************
*
.TRAN 	0.05US  4US 0 0.05US
.AC 	DEC 	20 0.1 1000MEG
.PROBE
.END

Top ↑

◄BACK TO OPAMP MODELS

© 2007 eCircuit Center