SAMPLING THEORY
CIRCUIT
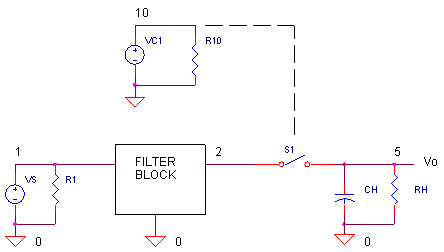
SAMPLING.CIR Download the SPICE file
For many reasons, continuous signals get sampled (converted to discrete-time digital signals by an Analog-to-Digital Converter). For example, you can take a number of temperature readings from a sensor and process them with a microcomputer. Not only can the samples be averaged to reduce noise, but accuracy can be improved by adjusting the sensor's non-linear curve. In another example - an audio DSP-based graphic equalizer - you can sample the audio signal, apply band-pass filters in the digital world, and then convert it back to continuous audio.
Sampling seems straight forward: acquire a stream of instantaneous values equally spaced in time. But beware - the sampled waveform can be deceiving! Things aren't always what they seem unless you know your input signal, a little sampling theory and how to choose an essential circuit in the chain, an anti-aliasing filter.
SAMPLE AND HOLD
Most sampling systems require a Sample and Hold Circuit - a series switch S1 and a hold capacitor CH - as shown in the above circuit. It works like this: S1 closes instantaneously (actually for 1 μs in this case) and charges up CH to the input voltage. When S1 opens, CH holds the input level until S1 closes again. It's during the "hold" time that an ADC converts the sampled level to a digital word. The sampling action repeats at the sampling frequency, fs = 20 kHz in this example.
CIRCUIT INSIGHT Run a simulation of SAMPLING.CIR. Source VS generates a 1 kHz sinewave. Source VC1 controls S1 by turning it on for 1 us every 50 μs (fs = 1/50 μs = 20 kHz). Although we've thrown in a filter block from nodes 1 to 2 for later use, now its simply a unity gain buffer. Plot the input signal V(2) and the sampled signal V(5). What do you see? It looks like the 20 kHz sampling frequency nicely captures the 1 kHz signal!
SAMPLING THEOREM
What about sampling a higher frequency sinewave like 5 kHz? Change VS to a higher frequency.
VS 1 0 SIN(0VOFF 5VPEAK 5KHZ)
What does V(5) look like now? The 5 kHz sinewave sampled at 20 kHz is still captured, but not quite as well! In fact there's a limit on the highest frequency that can be characterized by its samples. This limit is stated in the Sampling Theorem that says
Under ideal conditions, a sampling rate fs can
accurately capture input signals up to fs / 2.
What does this mean for our 20 kHz sampling rate? Inputs signals of 10 kHz and below can be faithfully sampled.
ALIASING
CIRCUIT INSIGHT Let's test the Sampling Theorem by setting VS to something beyond the fs / 2 limit like15 kHz. Rerun the simulation and check out V(5). Wow, its true, the 15 kHz cannot be found! In fact, what does it look like? The sampled waveform appears just like the 5 kHz signal! It seems the 15 kHz signal (sampled at fs = 20 kHz) is masquerading as a 5 kHz signal. You could say that 15 kHz has an alias of 5 kHz in this 20 kHz sampled world.
How can you predict the potential alias frequencies fALIAS of a particular signal fo given the sampling rate fs? Use this formula
fALIAS = n ∙ fs ± fo
where n = 1, 2, 3,... and check if any values fall below fs / 2. For the 15 kHz signal, fALIAS = 20kHz - 15 kHz = 5 kHz.
NOISE, INTERFERENCE AND ANTI-ALIASING FILTERS
Aliasing can spell trouble if there's noise and interference at frequencies above your fs / 2 limit. Some may wrongly advise, "Just filter out these unwanted high frequency signals using a digital filter after its sampled." But as we've seen, aliasing may fold these high frequencies right into the low frequency band where your signal of interest lies.
► The key to avoiding the problems of noise and interference is to apply
an Anti-Aliasing Filter to stop all signals above fs / 2 before they get sampled!
Ideally, stick a brick wall low-pass filter at fs / 2 before sampling and all is right with the world. But, because ideal filters don't exist, you'll have to choose one balancing the usual compromises of performance, complexity and cost.
HANDS-ON DESIGN Suppose there's interference a switching power supply operating at 25 kHz. Change VS to 0.5 Vpeak at 25 kHz and rerun a simulation. What frequency does it show up as in the 20 kHz sampled world? How big is it? This added signal could severely effect your signal measurements!
Now, bolt in an anti-aliasing filter ( 2nd-order low-pass filter) between VS and the Sample / Hold circuit. To do this, remove EBUFFER by placing a "*" in front of the it. Then, insert E_LPFILTER by removing its "*". To create the filters, the LAPLACE behavioral functions come in handy to implement a Butterworth Filter with cuttoff frequency fc.
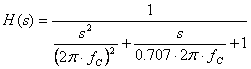
Now, take the system out for a test drive with the fc = 10 kHz. What has happened to the sampled 25 kHz interference signal at V(5)? Yes, its been dutifully squashed by the filter. But, before we go any further, does the filter have any adverse effect on the 1 kHz signal? Change VS to 5 Vpeak at 1 kHz and rerun a simulation. The desired signal should look as before.
HANDS-ON DESIGN But what if you need to reduce the interference further? You have a couple of options: either increase the order of the low-pass filter or lower the cutoff frequency fc. Try lowering fc to 5000 Hz by replacing all of the 10000 values with 5000 in the Laplace statement. Then check out the effect at V(5) for both the interference (0.5V at 25kHz) and the desired signal (5V at 1 kHz). Yes, the interference has been reduced, but, the 1kHz has experienced some phase delay from the filter.
If you can't tolerate any delay or attenuation of your desired signal, increase the filter order from a 2nd to a 4th and push fc back up to 10 kHz. To do this, add another 2nd Order Filter in the circuit chain. To keep the Butterworth response, change Q = 0.707 to 0.541 in both filters. If all went well, the interference should be reduced with less effect on the desired signal.
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extension.
SAMPLING.CIR - SAMPLING CIRCUIT
*
VS 1 0 SIN(0VOFF 5VPEAK 1KHZ)
R1 1 0 1MEG
*
* FILTER BLOCK
* NO FILTER
EBUFFER 2 0 1 0 1
R3 2 0 1MEG
*
* 2ND ORDER LP FILTER
*E_LPFILTER 2 0 LAPLACE {V(1)} {1/((s*s)/(6.28*6.28*10000*10000) + s/(0.707*6.28*10000) +1 )}
*
*
* SAMPLE & HOLD CIRCUIT
S1 2 5 10 0 SRES
CH 5 0 0.01UF
RH 5 0 10MEG
*
* S/H CONTROL VOLTAGE
VC1 10 0 PULSE(0V 5V 0US 0.1US 0.1US 1US 50US)
R10 10 0 1MEG
*
*
.MODEL SRES VSWITCH(VON=5V VOFF=0V RON=10 ROFF=10MEG)
*
* ANALYSIS
.TRAN 1US 1000US 0US 2US
*
* VIEW RESULTS
.PLOT TRAN V(2) V(5)
.PROBE
.END
© 2003-2005 eCircuit Center