Create Waveforms with
the Summing Amp + the Fourier Series
CIRCUIT
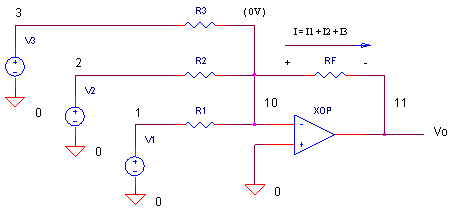
OPSUM.CIR Download the SPICE file
We saw in another topic how the summing amplifier enables you to add several signals together.
Vo = - RF ( V1 / R1 + V2 / R2 + V3 / R3)
= - ( V1 · RF / R1 + V2 · RF / R2 + V3 · RF / R3 )
Let's combine this amp with a little knowledge of signal theory to generate some waveforms.
FOURIER SERIES - SAWTOOTH WAVEFORM GENERATOR
You can create a basic sound synthesizer by adding a number of sinewaves to generate various waveforms (saw-tooth, square-wave, violin sound, clarinet, etc.) What is the exact recipe for a particular waveform? Fourier Analysis is a magical tool that takes a waveform (sound for example) and breaks it down into some basic ingredients: a sinewave at some fundamental frequency fo, plus, other sinewaves at harmonic frequencies 2 x fo, 3 x fo, and so on.
For example, to cook up a saw-tooth waveform at 100Hz, Fourier Analysis tells us the ingredients are as follows
V(t) = sin( 2π 100Hz t ) + (1/2) sin( 2π 200Hz t ) + (1/3) sin( 2π 300Hz t ) + ...
Only the first three terms of Fourier Series are shown here. To simulate them, you'll need three voltage sources, one at the fundamental and two harmonics.
* FUNDAMENTAL 100HZ + HARMONICS
V1 1 0 SIN(0V 1VPEAK 100HZ)
V2 2 0 SIN(0V 1VPEAK 200HZ)
V3 3 0 SIN(0V 1VPEAK 300HZ)
Next, the precise amount of each component has to be added together. From the Fourier Series, we see we need gains of 1, 1/2 and 1/3. These can easily be designed with R values like
* INPUT Rs
R1 1 10 10K
R2 2 10 20K
R3 3 10 30K
* FEEDBACK R
RF 11 10 10K
HANDS-ON DESIGN Copy the above voltage sources and Rs into the summing circuit (Comment out the initial voltage sources and resistors.) Then, take your home-grown saw-tooth waveform out for a spin. To get a better view, extend the Transient Analysis to 20 ms to see two cycles of the output. As you can see, with only three components of the Fourier Series, the waveform actually starts looking like a saw-tooth. Want a better looking saw-tooth? Add some more sinewave components following the pattern: V4 at 400Hz with R4=40k, V5 at 500 Hz with R5=50k, and so on.
SQUARE-WAVE GENERATOR
For a square wave, the Fourier Series looks like
V(t) = sin( 2π 100Hz t ) + (1/3) sin( 2π 300Hz t ) + (1/5) sin( 2π 500Hz t ) + ...
What's different about this recipe? Only the odd harmonics are needed (100 Hz, 300 Hz, 500 Hz,...) To simulate the square wave, take your saw-tooth generator and place a comment * at the beginning of the even numbered voltage sources and resistors, leaving only the odd ones. How many components do you need for a decent looking square-wave?
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extention.
OPSUM.CIR - OPAMP SUMMING AMPLIFIER
*
* SINEWAVE 4KHZ
V1 1 0 SIN(0V 1VPEAK 4KHZ)
* SQUARE WAVE 100HZ
V2 2 0 PWL(0MS 1V 5MS 1V 5.01MS -1V 10MS -1V)
* TRIANGLE WAVE 500HZ
V3 3 0 PWL(0MS -1V 1MS 1V 2MS -1V 3MS 1V 4MS -1V
+ 5MS 1V 6MS -1V 7MS 1V 8MS -1V 9MS 1V 10MS -1V)
*
* INPUT Rs
R1 1 10 10K
*R2 2 10 10K
*R3 3 10 10K
* FEEDBACK R
RF 11 10 10K
*
* OPAMP
XOP 0 10 11 OPAMP1
*
*
* OPAMP MACRO MODEL, SINGLE-POLE
* connections: non-inverting input
* | inverting input
* | | output
* | | |
.SUBCKT OPAMP1 1 2 6
* INPUT IMPEDANCE
RIN 1 2 10MEG
* GAIN BW PRODUCT = 10MHZ
* DC GAIN (100K) AND POLE 1 (100HZ)
EGAIN 3 0 1 2 100K
RP1 3 4 1K
CP1 4 0 1.5915UF
* OUTPUT BUFFER AND RESISTANCE
EBUFFER 5 0 4 0 1
ROUT 5 6 10
.ENDS
*
* ANALYSIS
.TRAN 0.05MS 10MS
* VIEW RESULTS
.PLOT TRAN V(11)
.PRINT TRAN V(11)
.PROBE
.END
© 2002-2010 eCircuit Center