OP AMP - MAX SLEW RATE
CIRCUIT
OP_SLEW_RATE.CIR Download the SPICE file
Entering the electronics field, one question quickly came to mind: Why
the mind-boggling variety of op amps in the databook? I discovered that a
key element of practical amplifier design requires choosing a device whose
limitations won't significantly degrade the signal of interest.
This degradation can appear in the form of distortion, clipping, DC offset,
noise, attenuation and phase (time) shift.
SLEW RATE MAX
One significant limitation is the maximum slew rate. This is simply the
fastest rate of change versus time that an amplifiers output can
move. You can write this as
∆V/∆t
max (volts per second)
Why worry about it? Try amplifying a square wave or sine wave without
considering the maximum slew-rate. The distortion that results can be
spectacularly disappointing. However, a couple of simple calculations can
lead you to the right engine for the race. In this topic you'll see the wrong
and right devices applied to amplifying square and sine waves.
SQUARE WAVE DRIVER
Suppose you've been asked to design an output buffer to drive the output of
a function generator (Sine, Triange, Square Wave outputs) The expectations
for the square wave are as follows: 10Vpeak and 50 ns rise time from 10% to 90%
of the final value. What's the minimum bandwidth and slew-rate you need
to make it happen?
BANDWIDTH
Assuming a single pole bandwidth for the op amp, there's a simple relation
between bandwidth fc and the 10% to 90% risetime, tr.
fc = 0.35 / tr
SLEW-RATE
You can estimate the slew rate with a simplified view of the
leading edge. Calculate the rising edge as a linear change between 10% and
90% of the step input.
We'll test this simplification later.
∆V/∆t
= (V10%-V90%) / tr
SINE WAVE DRIVER
Let's turn our attention to driving a sine wave of 10V peak and 2 MHz max.
BANDWIDTH
The goal is to leave the sine-wave unchanged at 2 MHz. The bandwidth
(single-pole low-pass filter response) affects a sine wave in two ways - it
decreases the amplitude (attenuation) and delays the signal in time (phase
shift). How much? Here's a table of gain and phase versus the ratio of f /
fc (where fc is the cutoff frequency of the filter.)
| f / fc | gain (V/V) | gain (dB) | delay (deg) | |
| 0.1 | 0.995 | -0.04 | -6 | |
| 1 | 0.707 | -3.01 | -45 | |
| 10 | 0.100 | -20.0 | -84 |
Setting your bandwidth to the sine frequency (fc = 2MHz) is obviously a bad idea. This cuts the 2 MHz signal down by 0.707 and delays it by an 1/8 of a wave (-45 deg). Instead try fc >= 20 MHz. The table above shows that at f / fc = 2MHz / 20MHz = 0.1, the low-pass filter response imposes only a small attenuation and delay.
SLEW-RATE
For a
sine wave with fo = 2 MHz and Vpeak = 10 V, how fast doest does Vo need to
change? Simply take the derivative of Vo = Vpeak·sin(2·π·fo·t) with respect to time.
dVo/dt = d/dt( Vpeak · sin(2·π·fo·t) )
= (Vpeak·2·π·fo) · cos(2·π·fo·t)
When the does the fastest slew occur? The greatest value for the cos term happens at t=0. (This makes sense! The sine wave slews the fastest when it crosses zero at t=0.) Therefore, the max slew rate is
dVo/dt max = Vpeak·2·π·fo
TEST RUN - SQUARE WAVE
Enough talking - let's start designing and testing. Reviewing our design, we
need to drive a 10V peak square wave and meet the rise time (10% to 90%) of
tr = 50 ns.
| Bandwidth | Slew-Rate | |
| fc = 0.35/tr = 0.35/50ns = 7MHz |
dVo/dt max = (V90% - V10%)/tr | = (9V-1V)/50ns = 160V/us |
Looking at your company's stock, you see two high speed devices in your company stock.
| Device | Gain Bandwidth Product | Slew-Rate Max | |
| OP_001 | 40MHz | 100 V/us | |
| OP_002 | 40MHz | 200 V/us | |
| OP_000 | 40MHz | No Slew Limit (Fantasy device) |
As far as bandwidth goes, all exceed the 7 MHz requirement. However,
regarding slew rate, only OP_002 clears the bar of 160V/us. Unfortunately,
the OP_002 is far more expensive. Therefore, you must convince the project
manager it's worth the money. I've included a fantasy device (no slew rate
limit) to demonstrate how an inexperienced engineer (like myself) once
walked down the path of self delusion.
CIRCUIT INSIGHT
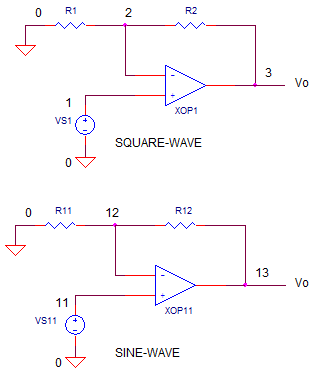
VS1 generates a step input. The op amp is defined
by a subcircuit in the statement
XOP1 1 2 3 op_000
where XOP1 is the op amp, nodes 1 and 2 are the inputs, node 3 is the output and OP_000 is the name of the subcircuit. You can find the actual subcircuit at the bottom of the netlist between statements.
.SUBCKT op_000 1 2 82
(op amp subcircuit components)
.ENDS
Initially, XOP1 is
defined by our fantasy device OP_000 - no slew limit. Run a Transient
Analysis and plot the input V(1) and output V(3). Notice how the output's
rapid change looks impressive rising in less than 10ns!
HANDS-ON DESIGN
But now replace the OP_000 (in the XOP1) statement with
the OP_001 (100V/us) - a more realistic device. Rerun the simulation and
watch reality come crashing down. The once rapid change is now constrained
by the max slew rate. V(3) struggles to rise in under 100 ns, falling short
of the 50ns specification. Finally, you reach for the OP_002 (200V/us) and
strap it in place of the OP_001. What happens at the output now? Does it
rise from 10% to 90% of full value in less than 50ns?
TEST RUN - SINE WAVE
Let's apply the same design process to driving a 10V peak square wave at
fo = 2 MHz.
| Bandwidth | Slew-Rate | |
| fc = 10 x fo = 10 x 2 MHz = 20 MHz |
dVo/dt max = Vpeak*2*pi*fo = 10*2*3.14*2M = 126 V/us |
Reviewing your stock of devices, it's clear which one is the winner. But, let's see
what the others do.
CIRCUIT INSIGHT
VS11 generates a 10V peak sine wave at 2 MHz.
Let's first live the fantasy and try OP_000 - no slew limit in XOP11. Run a
Transient Analysis and plot the input V(11) and output V(13). Notice the
sine wave looks beautiful except for a small time (phase) shift. Why? The op amp
has a finite bandwidth at 40 MHz. Even though the cuttoff frequency is
twenty times higher than 2MHz, there's till a bit of delay.
HANDS-ON DESIGN
Getting back to reality, let's try the OP_001 (100V/us). How
bad will this relatively "slow" device distort the sine wave? Swap the
OP_000 device for OP_001 and rerun the simulation. What happened to our
beautiful sine wave? OMG, it's been mangled into a triangle wave of sorts,
slewing up and down, but never quite keeping up with the input.
Finally, swap the OP_001 for the OP_002 (200V/us). That's better - the output swings pure and true like the input. This simple demo makes a compelling case: research + math + simulation = good design practice. The last step, of course, is actually building the circuit and hanging a scope at the output.
RELATED TOPICS
Find out how to create op amp models with
Slew Rate Limit.
or a description of all op amp models, see
Op Amp Models.
This op amp model can be used for many of the op amp
circuits available from the Circuit
Collection page.
SPICE FILE
Download the file
or copy this netlist into a text file with the *.cir
extension.
OP_SLEW_RATE.CIR
*
* SQUARE WAVE INPUT
VS1 1 0 AC 1 PWL(0NS 0V 1NS 10V)
*
* SIN WAVE INPUT
VS2 11 0 AC 1 SIN(0V 10VPEAK 2E6HZ)
*
*
* NON INVERTING AMP 1
R1 0 2 1000K
R2 2 3 1
XOP1 1 2 3 op_000
RL1 3 0 10k
* NON INVERTING AMP 2
R11 0 12 1000K
R12 12 13 1
XOP11 11 12 13 op_000
RL11 13 0 10k
* OP AMP MODELS *******************************
* Device Pins In+ In- Vout
.SUBCKT op_000 1 2 82
*
* INPUT R
RIN 1 2 1e9
*
* AMPLIFIER STAGE: GAIN, POLE, SLEW
* Aol=1000000, fu=40000000 Hz, Slew=100 V/us
G1 0 10 VALUE = { 2.51322e-3 * V(1,2) }
R1 10 0 3.97897e8
C1 10 0 1e-11
*
* OUTPUT STAGE
EOUT 80 0 10 0 1
ROUT 80 82 100
*
.ENDS
************************************************
* Device Pins In+ In- Vout
.SUBCKT op_001 1 2 82
*
* INPUT R
RIN 1 2 1e9
*
* AMPLIFIER STAGE: GAIN, POLE, SLEW
* Aol=1000000, fu=40000000 Hz, Slew=100 V/us
G1 0 10 VALUE = { LIMIT( 2.51322e-3 * V(1,2), +0.001, -0.001 ) }
R1 10 0 3.97897e8
C1 10 0 1e-11
*
* OUTPUT STAGE
EOUT 80 0 10 0 1
ROUT 80 82 100
*
.ENDS
************************************************
* Device Pins In+ In- Vout
.SUBCKT op_002 1 2 82
*
* INPUT R
RIN 1 2 1e9
*
* AMPLIFIER STAGE: GAIN, POLE, SLEW
* Aol=1000000, fu=40000000 Hz, Slew=200 V/us
G1 0 10 VALUE = { LIMIT( 1.25661e-3 * V(1,2), +0.001, -0.001 ) }
R1 10 0 7.95793e8
C1 10 0 5e-12
*
* OUTPUT STAGE
EOUT 80 0 10 0 1
ROUT 80 82 100
*
.ENDS
* ANALYSIS *************************************
.TRAN 0.1NS 500NS
*.AC DEC 20 0.1 1000MEG
.PROBE
.END
© 2010 eCircuit Center