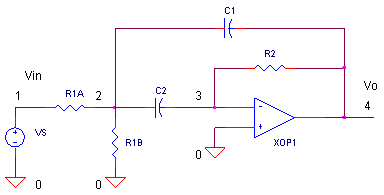
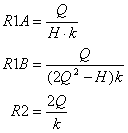Multiple Feedback Band-Pass Filter
CIRCUIT
MFB_BANDPASS.CIR Download the SPICE file
There's a couple of advantages to this active band-pass filter. First, you don't need an inductor (bulky and expensive at low frequencies) to create the band-pass shape. And second, it only needs one op amp device.
One disadvantage is the nature of adjusting the center frequency fo. Adjustments are not orthogonal (independent). You can tune fo with a resistor, but, the Q also changes. Still, the circuit is easy to implement and is useful for Q's up to about 20. But you've got to be aware how component tolerances alter your tuning frequency. And, you'll need an op amp with enough horsepower so it won't spoil your frequency response.
One application of this handy circuit is a graphic equalizer, created by feeding a signal to a number of parallel band-pass filters each tuned to a different frequency; typically octaves apart. Then, you can adjust the strength in each band via a front panel potentiometer. The outputs of all the filters are then summed to create overall frequency response of the equalizer.
BAND-PASS FILTERS
Band-pass filters are called into action to pass a range of frequencies only. How can you describe the filter shape? Here's a few ways.
Center frequency, fo. The center of the band, typically the peak of the frequency response curve.
Bandwidth, BW = fH - fL. The upper and lower frequencies, fH and fL, are defined as the frequencies where the gain has dropped to 0.707 of the mid-band gain.
Quality factor, Q = fo / BW. The Q tells you about the width of the pass-band:
Low Q → Wide bandwidth; High Q → Narrow bandwidth.Mid-band Gain, H = Vo / Vin. This is voltage gain at the center frequency fo.
MULTIPLE FEEDBACK BAND-PASS
You can visualize the band-pass nature of this circuit by inspecting its topology - R2 and C2 form a differentiator like circuit (high-pass), while C1 and R1A/B form an integrator like circuit (low-pass). Letting C1 = C2 makes the Multiple Feedback Band-pass filter straight forward to design. Just follow these simple steps.
Choose
C = C1 = C2.
then calculate k = 2 π fo C and
( Notice the role of k as a scaling factor for all resistors.) We'll let the rubber hit the road with a design example: choose fo = 10 kHz, H = 1 V/V and C = 10000 pF. Calculate R1A = 7.96 kΩ, R2A = 162 Ω and R2 = 15.9 kΩ.
CIRCUIT INSIGHT Simulate the SPICE circuit named MFB_BANDPASS.CIR. Plot the results of the AC Analysis by adding the input trace V(1) and output trace V(4). Does the AC response show the a 1 V/V peak at 10 kHz? What about the bandwidth? From our equation above Q = fo / BW, you can rearrange it to predict the bandwidth, BW = fo/Q = 10 kHz / 5 = 2 kHz. To measure the BW, put up a cursor to find the two frequencies where the gain drops to 0.707 V/V. You should locate them around 11 and 9 kHz, giving you the advertised bandwidth of 2 kHz!
HANDS-ON DESIGN Select new gain and Q values. Calculate the RC components and take your new filter out for a spin. Does the frequency response of the output voltage match your design goals?
COMPONENT VARIATIONS
So what happens if the exact resistor you calculated is not available? What about tolerance and temperature drift of the components you do have? You can get a feel for the effect of components variations on performance by the following equations. ( First calculate R1 = R1A || R1B.)
![]()
As an example, suppose R2 value differs by 5 % of the design value. What is the effect on tuning? From the equations, fo is a function of the square root of R2. So you can expect the center frequency to change by √5% or about 2.4 %. Increase R2 to 15.9 k x 1.05 = 16.7k and see what happens to fo. Use a cursor to get an accurate measure of fo.
If you need to precisely tune the center frequency, you could stick a potentiometer at R2. But as you can see from the upper right equation, the BW will also be effected. However, the exact bandwidth may not be as critical as the center frequency.
PHASE SPOTTING
Where exactly is the center frequency of this filter? There's two ways to find the tuned frequency of a band-pass filter: 1. Find the peak of the gain versus frequency curve. 2. Find the frequency where the phase goes through zero. The latter may come in handy for low Q filters where the peak is less pronounced. To watch the phase shift change versus frequency, add the trace VP(4) where P indicates Phase. The phase looks pretty much like your typical LCR filter, positive phase (inductive) below fo, zero phase at fo, and negative phase (capacitive) above fo.
But wait you say, you noticed the phase at fo does not go through zero, it goes through -180 degrees! Ah yes, the configuration of the op amp circuit is an inverting one. (Remember, another way of describing an inversion is to say its shifted by -180 degrees.) Therefore, all of the phase behavior is shifted by -180 degrees.
SETTLING TIME
How does the filter respond when you hit the filter's input with a burst of sinewaves? Does the circuit simply pass sinewaves with a magnitude indicated by the frequency response plot? As you might have guessed, nothing happens instantaneously in this universe. Run a simulation and plot Transient Analysis results. Add input and output traces V(1) and V(4). For the time analysis, VS produces a burst of sinewaves of 1V peak at 10 kHz. What do you notice about the output? Yes, it takes time for the output to settle to its steady state value. Does Q (or BW) influence setting time? Yes, you'll find a higher Q (narrower bandwidth) requires a longer settling time.
OP AMP HORSEPOWER
One of the most critical devices in achieving the band-pass function is the op amp. Specifically, it needs sufficient horsepower (gain and bandwidth) in the range of your design frequencies. The op amp in the SPICE file has Gain Bandwidth Product of GBP = 10 MHz. This appeared to be okay for fo = 10 kHz and Q =5. But, what about a design that calls for fo = 1 MHz?
HANDS-ON DESIGN Scale up the center frequency by a factor of 100 by reducing C1 and C2 from 10000 pF to 100 pF. Take the filter out for a test drive. ( Don't forget to increase the frequencies of the AC Analysis to 300 kHz - 3000kHz.) Did the filter achieve its goal with the current op amp? If not, pick a faster op amp with a GBP =1000 MHz by modifying the model. To increase its pole frequency FP1 by a factor of 100, just reduce RP1 from 1000 to 10 Ω. This new model should have enough muscle to produce the expected peak at 1MHz.
SIMULATION NOTE
The op amp is modeled using a subcircuit named OPAMP1. Although the guts of an op amp can contain 20 transistors or more, this model mimics only the higher level (or macro) functions of the device. The result is a simple model requiring only a handful of components. For a more detailed look inside, see the Basic Op Amp Model.
Subcircuits are handy ways of inserting a particular circuit into one or more places of the main circuit. They're easy to define and use. Check them out in Why Use Subcircuits?
SPICE FILE
Download the file or copy this netlist into a text file with the *.cir extention.
MFB_BANDPASS.CIR - OPAMP MULTIPLE FEEDBACK BAND-PASS FILTER * VS 1 0 AC 1 SIN(0VOFF 1VPEAK 10KHZ) * R1A 1 2 7.96K R1B 2 0 162 R2 3 4 15.9K C1 2 3 10000PF C2 2 4 10000PF * XOP 0 3 4 OPAMP1 * * * OPAMP MACRO MODEL, SINGLE-POLE * connections: non-inverting input * | inverting input * | | output * | | | .SUBCKT OPAMP1 1 2 6 * INPUT IMPEDANCE RIN 1 2 10MEG * DC GAIN (100K) AND POLE 1 (100HZ) * GBP = DCGAIN X POLE1 = 10MHz EGAIN 3 0 1 2 100K RP1 3 4 1000 CP1 4 0 1.5915UF * OUTPUT BUFFER AND RESISTANCE EBUFFER 5 0 4 0 1 ROUT 5 6 10 .ENDS * * ANALYSIS .AC DEC 200 3K 30K *.TRAN 1US 1000US * * VIEW RESULTS .PROBE .END
© 2002-2023 eCircuit Center